|
A New Metric to Detect
CO2 Greenhouse Effect By Slade Barker (24 July 2002)
Abstract The arid environment of New Mexico is examined in an attempt to correlate increases in atmospheric CO2 with an increase in greenhouse effect. Changes in the greenhouse effect are estimated by using the ratio of the recorded annual high temperatures to the recorded annual low temperatures as a measure of heat retained (i.e. thermal inertia, TI). It is shown that the metric TI increases if a rise in mean temperature is due to heat retention (greenhouse) and decreases if due to heat gain (solar flux). Essentially no correlation was found between the assumed CO2 atmospheric concentrations and the observed greenhouse changes, whereas there was a strong correlation between TI and precipitation. Further it is shown that periods of increase in the mean temperature correspond to heat gain, not heat retention. It is concluded that either the assumed CO2 concentrations are incorrect or that they have no measurable greenhouse effect in these data.
Introduction The ratio of the recorded annual low temperatures to the recorded annual high temperatures is used as the metric to measure greenhouse response. This ratio will be referred to as the thermal inertia, TI. This metric was chosen because it focuses on how effectively the atmosphere cools once the external source of heat is removed. The principal source of infra red radiation is solar during the daytime highs (out of the solar constant of about 1390 W/m2 [1], Approximately 415 W/m2 [2] are in the infra red portion) and terrestrial during the night-time lows. Like all greenhouse agents CO2 absorbs some of this radiation and radiates it back in random directions. Including some back towards the source. Thus the effects of this absorption and re-radiation as measured on the ground will be different. The daytime highs will be lower and the night-time low will be higher than they would have been without the moderation of the atmospheric greenhouse agents including CO2. This method has an advantage in that it offers a way to separate heating due to greenhouse effects and that due to increased solar radiation. The focus is on how things cool rather than how they heat. The greatest greenhouse agent is water vapor. An arid environment, which by definition has a low water vapor content, displays a wider range of temperatures than non-arid locals do. The heating and cooling in the arid environment of New Mexico provides a good example of this effect. In addition this lower water vapor content should also help separate and isolate the greenhouse effects of CO2. The choice of which New Mexico station sites to use was governed more by my recent visit to the area than by any scientific principal. Thus they are quasi-random selection, which more or less cover the whole state. While New Mexico has an arid environment, it is not devoid of water vapor. The recorded annual precipitation was used as an estimate of water vapor content. Precipitation only indicates the presence of water vapor; it is not a true measure of it. In addition the act of precipitation from the vapor state requires the loss of heat of vaporization. Nevertheless, it correlated well with the TI. In order to remove random errors inherent in individual stations and effects of the local environ’s thermal inertia, a simple regional least squares model is constructed. This model computes the regional average of a recorded parameter (i.e. high, low, mean temperatures, and precipitation) at the mean location of the stations, plus the spatial gradients of the parameter from the mean location. The vertical temperature gradient, the lapse rate, is one of the more interesting modeled parameters. The increase in this gradient over time would appear to be contrary to increased greenhouse effects. Further, the uncertainties associated with the regional average mean temperature are somewhat higher than the uncertainties associated with the global average mean temperatures published by the Intergovernmental Panel on Climate Change, IPCC, [3]. Because the area covered by this regional model is less than the five-degree squares used by IPCC in computing the global mean, and because it accounts for spatial gradients as well, these results are somewhat troubling and cast doubt on the small uncertainties used by the IPCC.
The Data The station data of the annual high, low, and mean temperatures, and the annual precipitation are from the U.S. Historical Climatology Network (USHCN) data set [4]. Only continuous consecutive year time series were used. This meant that different station series had different starting dates but they all terminated in 1994, the end date for the USHCN data set. The shortest series being Aztec Ruins station which had a beginning date of 1931 for its continuous consecutive records. The useful begin date was limited because of the short span of records of the atmospheric concentration of CO2. The earliest beginning date used was 1900. The atmospheric concentrations of CO2 were scaled from a NOAA CMDL [5] graph of the observed CO2 at Mauna Loa from 1958 to 1998. Inherent in the use of these data is the assumption of similar concentrations globally. The IPCC justifies this assumption as a consequence of a well-mixed atmosphere. The scaled values of concentration of CO2 were converted into the percent increase over 280ppm, which is assumed to be the pre-industrial level of the last millennium. A least squares exponential was fitted to the data and used to extrapolate back to 1900, at which point it was assumed that the levels of CO2 were near their pre-industrial level of 280ppm.
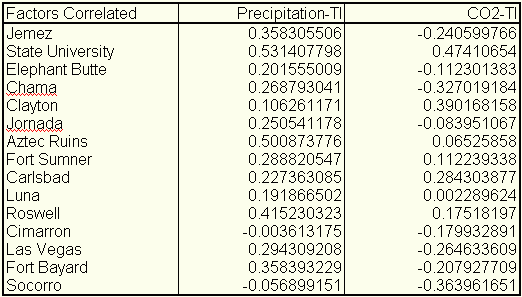
Analysis of station data The temperature data were first converted to degrees Kelvin. A TI series was computed for each station by simply dividing the annual low by the annual high. This quantity is then a measure of heat retained and is independent from the actual temperature. The correlation between the TI and the precipitation and CO2 data for each station was computed and presented in Table 1. The average correlation between the TI and precipitation is 0.26 with a variance of 0.16. The average correlation between the TI and CO2 is minus 0.02 with a variance of 0.25. The large variances are indicative of site-specific response (local thermal inertia) and/or errors. The phenomenon to be investigated is regional in nature and therefore must be regionally modeled. Table I
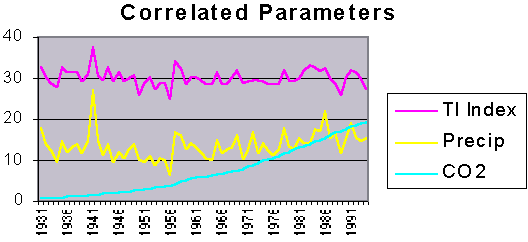
Regional Analysis To obtain a regional perspective and minimize random errors in the data of any particular station a regional model was constructed. First the mean position (q ,l ,Z) of the stations was computed. Here q is latitude, l is longitude, and Z is the elevation. The parameter being modeled (i.e. annual high and low temperatures and precipitation) and its spatial gradients are expressed as the following: Ti + (¶ T/¶ q )i · D q j + (¶ T/¶ l )i· cos(q)· D l j + (¶ T/¶ Z)i· D Zj = Oi,j .The index i refers to the ith year in the series, and the index j refers to the jth station form the set of stations. The unknowns to be computed are T, the modeled parameter of interest, (¶ T/¶ q ), its latitudinal gradient, (¶ T/¶ l ), its longitudinal gradient, and (¶ T/¶ Z), its vertical gradient. Oi,j is the observed parameter for station j at year i. The regional surface is approximated as planar rather than spherical. The error this induces in the spatial gradient calculations is negligible because of the small area. However, the longitudinal convergence must still be accounted for and that is why (¶ T/¶ l ) is multiplied by cos(q ). The difference of the jth station location and the mean location is given by (D q ,cos(q )· D l ,D Z) in meters. A least squares times series for the annual highs, lows and mean temperatures as well as the annual precipitation were computed. From these least squares derived time series TI was computed in the usual manner. As figure 1 illustrates, once individual station errors are minimized, there is a very strong correlation between precipitation and the TI of .77. However, the correlation between CO2 and TI is essentially nonexistent at -0.04.
Figure 1: The correlation coefficient between the precipitation and TI is .77 and between CO2 and TI is -0.04. The TI parameter has been adjusted to fit on the chart and illustrate the fine structure by removing the average multiplying by 10 and adding 30 (to move it off the zero bias line). The precipitation is in units of inches. The CO2 is in percent increase over 280ppm. All of this was done for visual effect and doesn’t effect the correlation coefficients at all. In addition to examining how atmospheric thermal inertia varies over time, the regional model allows the computation of the vertical gradients of the annual highs and lows. Figure 2 illustrates the results.
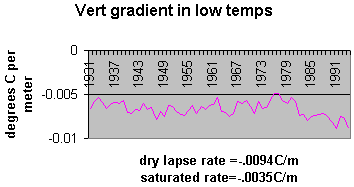
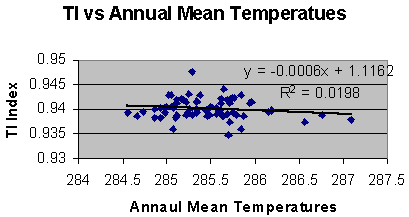
Figure 2: Modeled vertical gradient of annual low temperature. The units are in degrees centigrade per meter. Both the saturated and dry lapse rates are given of reference. As can be seen in figure 2 the regional model yields very reasonable results for lapse rates in an arid environment. It further illustrates a high vertical gradient, showing no evidence of enhanced greenhouse effect. The standard errors of the unknowns were computed from the covariance matrix. The standard error of the lapse rates averaged 0.0018oC/m. The IPCC [3] uses the annual mean temperature as a metric for global warming. This metric does not and cannot distinguish between an increase in heating (i.e. enhanced solar output) or a decrease in cooling (i.e. enhanced greenhouse effect). A regional model of the mean temperature for the above stations was computed. Because (q ,l ,Z) is the mean position of the stations it follows that: S j=1,15 D q j = 0, S j=1,15 D l j = 0, S j=1,15 D Zj = 0. Further because the coefficient of the unknown regional modeled mean temperature (i.e. T in the regional model equation) is always one, its computation is completely orthogonal to (i.e. independent of) the other unknowns. Therefore it is exactly the same answer one would get from taking the simple average of the stations mean temperatures. However, the standard errors for the two values are completely different. The reason that the standard errors are different is because even though the degrees of freedom for the regional model is only 11 and that for the simple average is 14, the gradient parameters provide for a much better fit. Thus the use of the smaller standard error is only valid if the gradients are used to compute the value anywhere other than at the mean position. If only the simple average is used over the region then larger errors will occur and the standard error of the simple average is applicable. The IPCC mean global averages are computed from 5X5 degree squares. The actual area covered in this study is smaller than a 5X5 degree square. When using global data there is always a trade off between data quality and availability. This means that the data comprising the global data set have data of uncertain and most likely lesser quality than that from a homogenous data set such as USHCN. The figures in the IPCC’s Technical Summary [3] imply a standard error of about .15 degrees centigrade. The regional model should yield smaller standard errors because it covers less area, it takes into account the spatial gradients, and the USHCN database is quality controlled. However the average standard error of the regional model is 0.27 degrees centigrade, and the standard error for the simple average is 3.4 degrees centigrade. How does IPCC justify such small standard errors? How well does the mean temperature metric reflect a change in the thermal inertia of the atmosphere? Figure 3 is a comparison between the regional annual mean temperature and the raw regional annual TI. It is clear that there is little correlation between them. To further investigate the nature of the different metrics, the regional modeled mean temperature is compared to the model deduced TI from 1973 to 1994. This period was chosen because it is a period of global mean temperature increase of the lower atmosphere as measured from radiosondes [6].
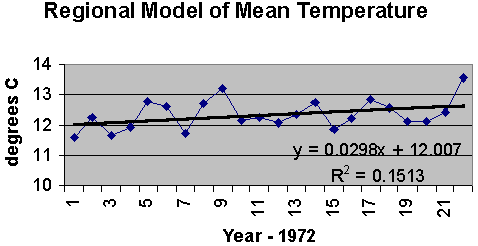
Figure 3: A scatter diagram between the regional modeled annual mean temperatures and the thermal index computed from the regional modeled annual high and low temperatures. Figure 4 illustrates that this increase was also measured at the stations as reflected by the regional model. The linear fit equation shows an increase of about 0.3°C per decade, and a correlation, R, of about 0.39.
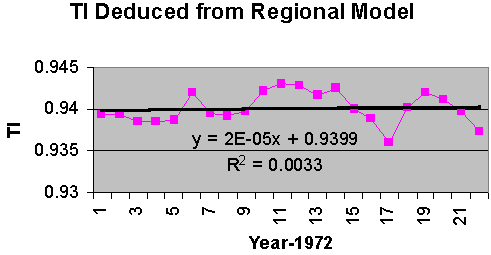
Figure 4: The regional model of the mean temperature as recorded in the USHCN data set. Figure 5 is a plot of the TI for this same period. While the linear fit of the TI for this time period appears to be increasing every so slightly, the goodness of fit is almost zero. The curves themselves appear to be out of phase. In fact the correlation coefficient between the two metrics over this period of time is -0.22.
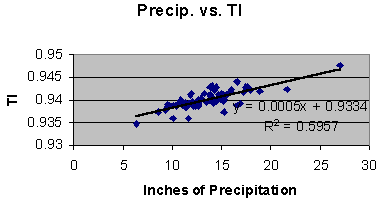
Figure 5: The thermal inertia computed from the regional modeled annual high and low temperatures. It is clear from figure 4 and 5 that the metrics of TI and mean temperature are behaving differently. The strong correlation between precipitation and the TI metric (as seen in figure 1) indicate that this metric is properly reflecting variations in the greenhouse agent of water vapor, even though precipitation is only an indication of water vapor not a proper measure of it. Nevertheless, with such a strong correlation it should be possible to model the relation with some confidence, and thus remove its effects on the TI series. Figure 6 is a plot of TI as a function of inches of precipitation.
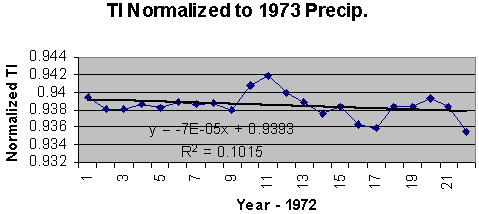
Figure 6: Thermal inertia vs. regional model of precipitation. As seen in figure 6 the rate of change of TI per inch of precipitation is: D TI/D Precipitation = .0005/inch .The above relation can be used to normalize the TI series in figure 5 to the 1973 precipitation, thus removing the effects of changes in precipitation from the series. The normalization is as follows: NTIi+1973 = TIi+1973 + .0005*(Precip1973-Precipi+1973). The result is displayed in figure 7.
Figure 7: The regional inferred TI normalized to the 1973 precipitation. By normalizing to the 1973 precipitation the greenhouse effect due to changes in precipitation is removed. Now the series clearly shows a negative trend. As will be shown below this is consistent with an increase in input energy rather than an increase in heat retention (i.e. enhanced greenhouse effect). The correlation coefficient between the regionally modeled mean temperature and the normalized TI is -0.49. To examine how TI varies as a function of solar variation the USHCN records of State University and Chama are examined for the winter months and the summer months. These data are continuous from 1882 to 1994 and 1890 to 1994 for State University and Chama respectively. It is clear that the incident solar energy per square meter is less in the winter than the summer, and it should be just as obvious that the temperature in the winter is less than that in the summer. The summer nights are shorter than the winter nights so the period of cooling is longer in the winter than in the summer. Further the water vapor that can be absorbed into the atmosphere is a function of the temperature. These seasonal variations in the data are assumed to be averaged out when using the annual means for the high and lows. In determining how TI responds to changes in seasonal energy input the differences in the length of night and the variation in absolute humidity must be accounted for. A first order estimate of the adjustments for difference between the lengths of summer and winter nights is made by assuming a constant cooling rate. In general this is not true but because the temperature gradient between the lower troposphere and the stratosphere (spatial gradient) is large compared to the cooling at the surface (temporal gradient), an assumed constant rate of cooling should not lead to large errors. TI computed as a function of cooling rate, CR, is: TI = Low/High = (High-CR*length of night)/High. As seen from the above relation the TI computed from the summer month averages will be significantly higher due to the shorter length of night. To examine how TI varies as a change in energy input a correction for the shorter cooling period must be made. If Rt represents the ratio of the winter to summer lengths of night then the adjustment for shorter cooling period is given by: TIsummer adjusted = TIsummer*Rt + (1-Rt). For State University station the value of Rt is 1.44 [7] and for Chama station it is 1.56 [7]. For TI values of about 0.94 this implies a correction of about a minus 0.02. A secondary correction was made for the increase in absolute humidity with an increase in temperature. Again precipitation was the only indicator of water vapor. To estimate the change in water vapor content as a function of temperature and precipitation a new indicator of absolute humidity at the average seasonal highs times the precipitation was used. The difference between the new indicator for the summer and winter months was computed. Because the absolute humidity is given in gm/m3, all precipitation was converted from inches to meters. The new scaling factor changes from 0.0005 units of TI per inch of precipitation to .0092 units of TI per m2/gm of the new water vapor indicator. This correction resulted in a decrease in the summer TI of about 0.001, or about a twentieth of the correction for change in the length of night. Figures 8 and 9 illustrate how TI changes as a function of input energy after adjusting the summer TIs for the shorter cooling period and greater water vapor content.
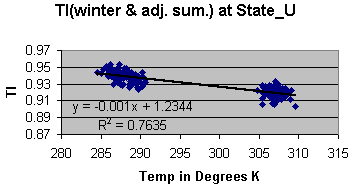
Figure 8: Variation is TI as a function of seasonal highs at State University Station.
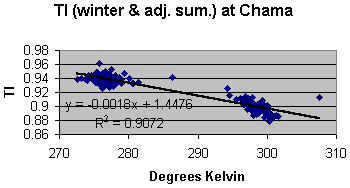
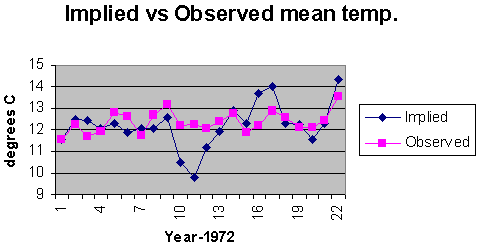
Figure 9: Variation in TI as a function of seasonal highs at Chama station. In both cases TI decreases with increases of input energy. The different rates are most likely due to a difference in the thermal inertia of the local environment of each station. The average decrease from the above figures is minus 0.0014 units of TI per degree Kelvin. Each seasonal data set (i.e. State University summer highs, State University winter highs, Chama summer highs, etc.) can be separately correlated to TI as well. The average decrease computed from a separate linear fit to each seasonal at each station is minus 0.00157. This is in good agreement with the minus 0.0014 figure. These numbers suggest that the drop in TI of figure 7 correspond to an energy increase, which should account for a rise in temperature of about 0.95°C. The trend of temperature rise in figure 4 suggests an observed increase of 0.68°C. The NTI series of figure 7 is normalized to the 1973 precipitation. Assuming that this accounts for the majority of change since 1973 in greenhouse effect, successive differences in the NTI values therefore represent changes in input energy. The implied corresponding changes of temperature can be computed from the following: D Tj = (NTIj – NTI1973)/(-.0014), for j = 1973,1974,...,1994. By adding these D Ts to the 1973 value of the regional modeled mean temperature, a temperature history consistent with changes in NTI can be constructed. Figure 10 illustrates the temperature changes that are implied by the decreases in the NTI series. The data are superimposed to compare the implied with the observed mean temperatures over this time period. The correlation coefficient is now 0.49. The implication is that the observed increase in mean temperatures over this time period is due to heat gain (i.e. increases in input energy) and not heat retention (i.e. greenhouse effect). The standard error from the covariance matrix for the regional model of the mean temperature (the observed portion of figure 10) is 0.49°C (not to be confused with the correlation coefficient between the implied and observed temperatures of figure 10, which is also 0.49). Using this standard error for a 3-sigma rejection filter on the residuals between the implied and the observed, the standard deviation of the residuals is 0.5, in good agreement with the standard error of the observed temperatures. The large departure (greater than 3-sigma) around 1981 between the implied and observed mean temperatures is most likely a reflection of thermal inertia not related to precipitation and therefore not removed by the normalization process.
The magnitude of this departure is much larger than the uncertainties of either the modeled mean temperature or the uncertainties in the correlation between precipitation and TI. Therefore it must be the result of something other than precipitation. Further it exhibits the characteristics of an underdamped response to an impulse stimulus. Perhaps a local increase in atmospheric aerosols could account for this anomaly? A search of the NOAA National Geophysical Data Center’s web site [8] for all volcanoes with an explosive magnitude of 4 or greater between 1973 and 1994 turned up 16 events. Of the 16 only 4 were less than 1500 miles away from the regional model’s center. These were Fuego (10/10/74, 1,450 miles away), Mt. St. Helens (5/18/80, 1,022 miles away), and El Chichon (once on 3/28/82 and again of 4/4/82, 1,232 miles away). Of these three El Chichon corresponds most closely with the initial departure between the observed and implied mean temperatures of figure 10. If aerosols associated with the El Chichon eruption were the stimulus, the response mechanism is still unclear. A few last observations on TI and CO2: It should be noted that the metric, TI, is bounded between 0 and 1. Therefore any expression relating its behavior will have to be asymptotic as either extreme is approached. All the above relations were linear approximations and never used to extrapolate beyond the boundaries of the input parameters. Secondly it is noted that the increase in CO2 is monotonic. Therefore any phenomena which is monotonic (i.e. the population, the world economy, the number of scientific papers on greenhouse effect) will correlate with the increase in CO2, a positive correlation if increasing and a negative correlation if decreasing.
Conclusion It has been shown that the metric TI correlates well with the greenhouse effects of water vapor as indicated by precipitation. It was further demonstrated that TI could be used to discriminate between an increase in atmospheric thermal inertia (greenhouse effect) and an increase in input energy. This property was used to demonstrate that the warming trend between 1973 and 1994 was due to increases in input energy and not increases in thermal inertia. There was no significant correlation between the rise in CO2 and the TI metric. The lack of correlation between the rise in CO2 and TI, suggest either the rise in CO2 has not appreciably increased any greenhouse effect, or atmospheric CO2 has not been increasing over New Mexico. Assuming a well-mixed atmosphere the lack of correlation between CO2 and TI is troubling. The TI metric is sensitive to changes of at least tenths of a degree. Therefore any change in the temperature due to increased atmospheric CO2 inhibiting cooling has been less than a tenth of a degree over this time period. In any event as more and more CO2 is added to the atmosphere the corresponding increase in greenhouse effect will become less and less until total absorption is reached at which time further additions of CO2 will have no effect. Thus we would expect the greatest detectable greenhouse response early on rather than later as it approaches total absorption. If the concentration of atmospheric CO2 is insufficient to absorb all the infrared energy in its excitation bands and there is an increase in CO2 but not in TI, then it may be that the effective excitation bands bandwidths are so narrow there is no appreciable energy retained. Conversely, all radiated energy in the excitation bands may already be absorbed. This may especially be the case if there is any overlap between the absorption bands of water vapor and CO2. In this scenario, because all the energy in the bands is absorbed, further increases in CO2 will have no additional greenhouse effect. The implication would be that the pre-industrial concentrations of atmospheric CO2 were already close to saturation (total absorption) levels. The TI metric and New Mexico data do not support the IPCC’s conclusion that increases in atmospheric CO2 play a significant roll in global warming. It is interesting to note that a 0.6% increase in the solar output would correspond to about 0.6°C increase in global temperatures using the Stefan-Boltzmann law and a solar radiance of 1,390 W/m2. References
About the Author Slade Barker retired as Director of the Data Processing and Validation Department of the U.S. Naval Oceanographic Office after 32 years of service in the U.S. Naval Oceanographic Research and Development Activity (now part of the U.S. Naval Research Laboratory) and the U.S. Naval Oceanographic Office. During this time he was associated with the American Geophysical Union, the International Union of Geodesy and Geophysics, and the International Association of Geomagnetism and Aeronomy, specializing in the modeling of the geomagnetic field from which the 5 year epoch magnetic variation charts were published by the U.S. Defense Mapping Agency and the British Hydrographic Office, and in gravitational field modeling in support of various naval weapon systems. Return to Climate Change Guest Papers page Return to "Still Waiting for Greenhouse" main page |