The Excel sheet shows the diagram
and automatically displays the parameters. After any change the resulting
curves are automatically updated, so you can easily try out all kinds of
variants. I append two Excel 97 files using a proper Bern
model simulation for SRES A1 and WRE550. The parameters are
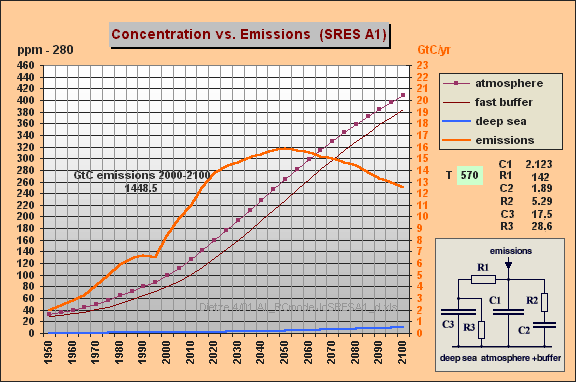
C1 = 2.123
GtC/ppm (atmosphere)
R1 = 142
ppm/GtC/a (R1*{C1+C2} yields T=570 yr)
C2 = 1.89
(fast aux buffer for BF=53%, C2 is 47% of C1+C2 or equivalent to 89% of
an additional atmosphere)
R2 = 5.29
(for fast aux buffer, yields T2=R2*C2=10 yr)
C3 = 17.5
(15.4 deep sea including 2.1 biomass sink, yielding 10% remanent fraction
[compare your 1993 Vegetatio paper])
R3 = 28.6
(T3=C3*R3=500 yr for sedimentation)
Displayed are the parameters
(sheet col B), the curves for emissions in GtC/yr (col C or D), the atmospheric
increment in ppm (col E), the increment for the aux buffer (col F) and
the increment for the deep sea (col G). You can see that
the deep sea part is very small and does **not** explain at all the differences
in our prognoses as you assumed. These are *only* explained by the 570yr
time constant that is implicitely used by the Bern model - together
with a larger aux buffer of a 89% (instead of 33%) atmosphere capacity.
My both simulations for SRES A1 and WRE550 nearly give *identical* results
as the Bern model.
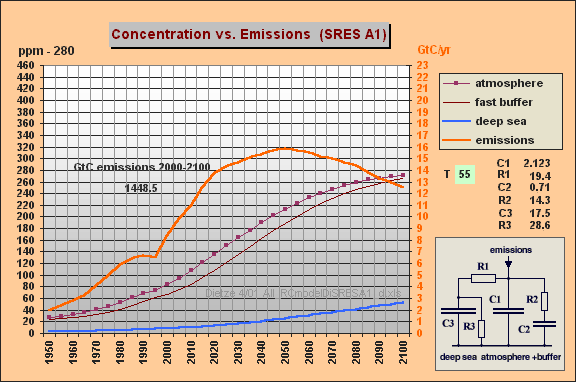
You can easily produce my
model (and related responses) if you enter
C1 unchanged 2.123
R1 = 19.4 (R1*{C1+C2}
yields
T=55 yr)
C2 = 0.7 (fast aux buffer
for buffer fraction BF=75% , i.e. C2=25% of
C1+C2)
R2 = 14.3 (yields T2=R2*C2=10
yr)
C3 unchanged 17.5 (yielding
10.5% remanent fraction)
R3 unchanged 28.6
The result for SRES A1 with these
model parameters is indeed similar as in my Web paper (Fig.5 => max 540
ppm). For WRE550 my former final 317 ppm (Fig.6)
are ocean-shifted to 360 ppm (in contrast to 550 ppm). So IPCC's
stabilization increment is still by a factor 3.4 too high. Hoping
you have much fun and insights studying my useful "All-RC-Model".
Best regards,
Peter
~~~~~~~~~
Here are the responses for
SRES A1 with the concentration for yr 2100, increasing to 689 ppm
when using Bern parameters and to only 551 ppm with T=55 yr. The deep sea
response for yr 2100 is merely 12 ppm with Bern parameters, but makes 53
ppm when T=55 yr is used.
Carbon Model Calculations
Tue, 10 Apr 2001 13:29:53 +0200
From: Lars Kamél <lars@internetami.se>
To: daly@microtech.com.au Fwd: p_dietze@t-online.de
I have looked at the theory behind
the IPCC models, and finally I think I understand it. The idea is that
when the CO2-content of the atmosphere increases, the nature (or at least
the ocean) adjusts by increasing the equlibrium value, that is, the CO2-level
where the natural outgassings and uptakes would be equal. If the antropogenic
emissions would stop, the CO2-levels would decay toward the equilbrium
value with a short lifetime (maybe 55 years as Peter Dietze found). But
the equilibrium value would also decay, toward the pre-industrial equilibrium
value, with a lifetime of several thousand years, because CO2 will slowly
be accumulated into the ocean sediments. This is why they talk about several
lifetimes. It is remarkable that both Peter Dietze and Jarl Ahlbeck find
that the present equlibrium value is the same as the pre-industrial. Shouldn't
the increase have started already?
Best regards,
Lars Kamél
Re Carbon Model Calculations
From: p_dietze@t-online.de To:
"Lars Kamél" <lars@internetami.se>, daly@john-daly.com
Lars, you should not misinterprete
the perturbation state as a shift of equilibrium. We consider the (final)
equilibrium towards which any concentration increment will "decay" to 1/e
within 55 years, as constant, i.e. 280 ppm. The equilibrium is *not* expected
to shift within the geological short time of fossil fuel use - consider
the huge oceanic sink capacity including shells and corals. When IPCC people
talk about several lifetimes, they consider a fast one (about 30 years
at the beginning, caused by buffering processes), then a medium one of
50..120..200 years for the main sequestration and a long one for the "tail".
I consider the reason to be the flawed eddy diffusion approach. With my
simulation I proved that the Bern model uses an "effective" 1/e lifetime
of 570 years (if the continuous uptake flux ist considered).
Sincerely,
Peter Dietze
Re: Re Carbon Model Calculations
Wed, 11 Apr 2001 11:36:24 +0200
From:: Lars Kamél <lars@internetami.se>
To: 091335371@t-online.de
Dear Peter,
I find the theory hard to understand.
One reason is that I haven't looked at chemical reaction and reaction rates
for 20 years. Evidently, the theory says that the fewer CO3(2-) ions there
are left in the ocean water, the harder it will be for the ocean to take
up more CO2. To me, this seems to be the same as saying that the equilibrium
value for the ocean is going up when the atmospheric content of CO2 raises.
And this theory is only about the inorganic uptake, while it should, in
fact, be the organic uptake that dominates.
Yours sincerely,
Lars Kamél
Re: Re Carbon Model Calculations
Wed, 11 Apr 2001 15:54:41 +0200
From: "P. Dietze" <091335371@t-online.de>
To: Lars Kamél <lars@internetami.se>
Lars, you seem to misunderstand
the procedure.
> To me, this seems to be the
same as saying that the equilibrium value
> for the ocean is going up
when the atmospheric content of CO2 raises
The oceanic content of CO3(2-)
ions is so gigantic that any anthropogenic CO2 impulse injected into the
atmosphere can be absorbed. But as there is a "resistance" of transport
and reaction, and proceeding to deeper water takes time, we observe an
1/e-lifetime of 55 years (or half-life time of 38 years) for the concentration
increment caused by an emission impulse. Note that we do not permanently
increase the atmospheric concentration (which would require huge amounts
of CO2 and theoretically slowly shift the oceanic equilibrium over millenia
as you indicated), but we only consider the emission of a certain limited
amount of CO2 - or a series thereof.
Sincerely, Peter
CO2 excess lifetime
and C14 puzzle
Sat, 21 Apr 2001 14:15:22
+0200
From: "P. Dietze"
<091335371@t-online.de> To: broecker@ldeo.columbia.edu
Dear Dr. Broecker,
My discussion is because
of my 55 yr CO2 lifetime parameter used in
my carbon model and my new paper "Carbon Model Calculations" at http://www.john-daly.com/dietze/cmodcalc.htm
- in contrast to the over ten times 570 yr e-fold
excess lifetime used by the Bern model (and the calculated graphs
for the IPCC TAR) - see especially Fig. 5, 8 and 9.
In an old contribution
in NATURE 370, 21 July 1994 "Imbalance in the budget"
Dr. Joos comments the main article by Hesshaimer, Heimann and Levin about
radiocarbon tracer evidence suggesting a 25% smaller oceanic carbon sink
than previously believed. I got stunned about Dr. Joos' statement on p.182
<< First of all, the equilibrium time between
surface water and air is about ten times longer for 14C than it is for
anthropogenic CO2 >>. Acc. to my parameter this should then be 550
years in comparison to the atmospheric figure of 16 years. I
wonder whether these 550 (or 570) years were taken in the Bern model for
the atmospheric C12.
This is why I checked
your 1993 textbook "Greenhouse Puzzles Part I"
(your GEOSECS figure from p.24) where you say "now after 30 years after
the peak, the C14/C ratio has fallen to just 14% above the pre-industrial
value" (p.19). This matches about a half-life time
of 16*ln(2)=11yr.
Do you have an explanation
for Dr. Joos' puzzling conclusion? I have the impression, there
may be some "misunderstanding factor". It is peculiar that there
is twice about a factor ten between turnover time (5yr), my e-fold lifetime
(55yr) and Dr. Joos' (570yr). And the observed C14 lifetime is just by
a factor 3 higher than the turnover time, and a factor 3.4 lower than my
55yr. I wonder how a factor 35 has obviously been
applied for calibration in the Bern model. Do you have any explanaition
for that?
With best regards,
Peter Dietze
Dipl.-Ing. P. Dietze
D-91094 Langensendelbach,
Germany
Phone&Fax +49/9133-5371
Email alias
p_dietze@t-online.de
(This
is the second attempt to get support from Dr.Broecker. Similar questions
have been sent to Prof. Goudriaan, Dr. O'Neill and Dr. Harvey - so far
no responses)
Carbon Model Calculations (discussion for http://www.john-daly.com/dietze/cmodcalD.htm)
Thu, 03 May 2001 15:06:41 +0200
From: "P. Dietze" <091335371@t-online.de>
To: daly@john-daly.com, bconeill@brown.edu, Bolin <bert.r@osteraker.mail.telia.com>,
Oppenheimer <michael@edf.org>, joos@climate.unibe.ch, Jan.Goudriaan@pp.dpw.wau.nl,
harvey@cirque.geog.utoronto.ca, wigley@meeker.ucar.edu, broecker@ldeo.columbia.edu,
peng@aoml.noaa.gov, ....
Dear John and others,
I analyzed the TAR excerpt that Dr. Volz sent (comprising
the puzzling statement of Dr. Joos in NATURE 370, 21 July 1994)
> 14 C has an equilibration time
with the atmosphere 10 times slower than CO2
and came to the conclusion that here the adjustment
time of the *ocean* is meant for an assumed constant increment in atmospheric
concentration. But this is not the time that
an emission impulse needs to be sequestered. When I consider Prof.
Bolin's text, it appears that the factor 10 for the CO2 excess lifetime
may
be caused by the Revelle factor.
> The latter changes the chemistry of the surface water
and the uptake therefore is hampered
> in that it is the transfer by
turbulence into deeper layers that determines the rate of uptake.
> This effect is absent in the
case of C14, which permits a much quicker uptake. This is implicit
> in all carbon cycle models if the buffering factor
(about 10) is properly incorporated
The IPCC-related modellers may have
applied the Revelle factor twice:
i) Revelle is *included* in the observation of C14 uptake
(!) which is indeed subject to [present] ocean chemistry - though
it is thought NOT to be - as Prof. Bolin said
ii) C12 was calibrated with C14, so they must have applied
Revelle to C12, not realizing that C14 is already subject to Revelle, as
it chemically behaves in the same way as C12.
As my CO2 excess lifetime parameter of 55 yr is merely
based on global sink flow observation, I suppose the
570 yr parameter applied in the Bern model should be on the erroneous side,
as it was likely derived theoretically and thus may contain the Revelle
factor twice. Any comments are welcomed.
Best regards,
Peter
RE: Carbon Model Calculations (discussion for http://www.john-daly.com/dietze/cmodcalD.htm)
Fri, 4 May 2001 10:04:31 +1000
From: "Enting, Ian" <ian.enting@dar.csiro.au>
To: "P. Dietze" <091335371@t-online.de>, daly@john-daly.com,
bconeill@brown.edu, Bolin <bert.r@osteraker.mail.telia.com>, Oppenheimer
<michael@edf.org>, joos@climate.unibe.ch, harvey@cirque.geog.utoronto.ca,
wigley@meeker.ucar.edu, broecker@ldeo.columbia.edu, peng@aoml.noaa.gov,
Taro Takahashi <taka@ldeo.columbia.edu>, Sarmiento <jls@splash.princeton.edu>,
bender@geo.princeton.edu, d.schindler@ualberta.ca, Hesshaimer <hr@uphys1.uphys.uni-heidelberg.de>,
.....
The time-response of the Bern model
is documented in the CSIRO technical paper 31 that we put out to
document the calculations reported in the 1995 IPCC radiative forcing report.
This is now available on-line at www.dar.csiro.au/publications/enting_2001a0.htm
(this is an index file that lets you select individual chapters as pdf).
The IPERT case of table 9.4 (from chapter
9) shows the long time-scale part for perturbations about CO2 levels higher
than preindustrial.
Probably the easist way to get a simplified view of what
the Bern model is doing is to use the mixed layer responses that the Bern
group have calculated (and published) and treat the non-linearities in
the partial pressure to carbon content explicitly. This will also let you
see what is happening to C14.
In discussing C14, you need to avoid confusing the description
of C14 with the description of the 'delta' which are differences in ratios.
It
is the deltas that have the timescales longer than CO2. There is
a very clear description of how the same issue applies for C13 in methane,
by Tans in Global Biogeochemical Cycles vol 11, pp77-81 (1997).
Re Carbon Model Calculations (discussion..)
Tue, 08 May 2001 13:21:00 +0200
From: "P. Dietze" <091335371@t-online.de>
To: Enting <ige@dar.csiro.au>, daly@john-daly.com,
joos@climate.unibe.ch
CC: bconeill@brown.edu, Bolin <bert.r@osteraker.mail.telia.com>,
Oppenheimer <michael@edf.org>, joos@climate.unibe.ch, ....
Dear Dr. Enting,
thanks for your important info!
> The time-response of the Bern model is documented in
the
> CSIRO technical paper 31... IPERT
case of table 9.4
I was not aware of this though I hold the 1994 CSIRO TP
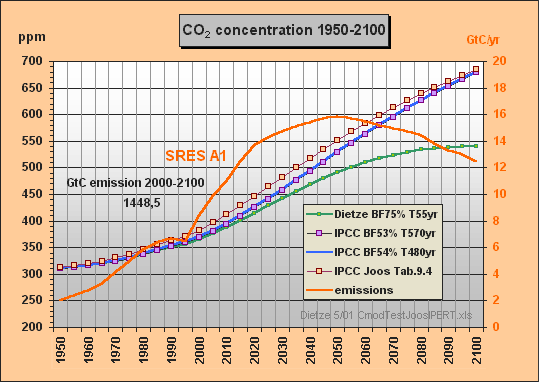
31. Now I have calculated the SRES A1 case using Excel and my sequential
convolution integral approach for t=5 yr intervals with following parameters
of the normalized Joos-IPERT response function:
G(t) = 0.297144 + 0.135191 exp(t/506.977719)
+ 0.365643 exp(t/16.5172219) + 0.202022 exp(t/3.054167)
Note the 507 yr lifetime part and that the
normalized sum of factors (including the remanent fraction of 29.7%) is
exactly 1.0. You can see the calculated response in the appended graph,
denoted as "IPCC Joos Tab.9.4". I started
the integration from the 280 ppm equilibrium in 1840, the display before
1950 is truncated. As the response is not identical with the TAR response,
I suppose Dr. Joos has slightly modified his parameters since 1995 - a
comment of his would be welcomed. Important to mention that the
sum of e-functions is from a set of linear differential equations, thus
representing a *linear* system, and so the response function can
indeed be normalized and correctly convolution-integrated for any arbitrary
perturbation signal.
This means (believe me as a control engineer, having worked
about this topic in my master thesis) that any perturbations and system
states can be superposed (i.e. added) *linearly*. So, for example, if you
take a perturbation scenario A, the equilibrium response for A, and a perturbation
B and the response for B, you would get the response
A+B for a perturbation A+B. Thus you should get *the same* additional
impulse response, no matter whether you use the pre-industrial equilibrium
or the S650 perturbation as base case.
I thus do not understand the different responses in Fig.
9.1 and 9.2 on p.35. I am wondering whether a different, may be a
full eddy nonlinear ocean diffusion model has been used to solve
for the perturbation case - similar to the different results for the linear
response and the full model shown in the Maier-Reimer
& Hasselmann paper about transport and storage of CO2 in the ocean
in Climate Dynamics 2, 63-90, 1987. I would be grateful for a comment.
Re the IPERT response function parameters I would like to note:
i) The Bern remanent fraction of
29.7% is far too high. Compare my 'All-RC-Model' capacitors in the
two SRES A1 Excel graphs above in this Web discussion. The ocean capacitor
C3 - I take a Revelle factor of 9 - is 39,000/9/280=15.5 GtC/ppm plus some
2 GtC/ppm for the woody biosphere. Take the ratio 2.123/(17.5+2.123+1.89)
and you get 10.1% for the remanent fraction - if
you leave out sedimentation, shells and corals. As your models only
consider the atmosphere as buffer and leave out my C2, you should apply
10.8%. Prof. Goudriaan used 11% with biomass included. With my parameter
set (BF=0.75) I get 10.4%.
ii) In my graph the blue curve calculated with my simple
model equation dC/dt = 0.54 E - C/480 (assuming
an infinite ocean capacity) is the same as the response from dC/dt
= 0.53 E - C/570 (IPCC simulation) and the same
as the black TAR response curve in Fig.5 of ../cmodcalc.htm. This
shows that - depending on the buffer fraction (BF is the ratio of atmosphere
to atmosphere +aux buffer, here 54 or 53%) - the effective CO2 excess lifetime
is *480 to 570 years*. Contrary to Dr. Joos' opinion the response (and
not only for SRES A1) can indeed be well simulated with my simple model
and *only two* parameters.
Surprisingly - in contradiction
to all cited CO2 lifetime assertions about 100 or 120 years - the effective
Bern CO2 excess lifetime is around 500 years, though the 507 yr fraction
in the IPERT response function is only 0.135. Foolishly you can
calculate a "weighted mean" of 0.135*507 +0.366*16.5 + 0.2*3.0
and thus get 75 years which is completely wrong. In the same way the response
function Go (eq. 9.2) on p.34 yields 100 years lifetime, which may
be the erroneous mean value often cited. I
am sure that if it was known, IPCC's e-fold lifetime effectively being
some 500 years (instead of 55), and the carbon models been comprehensively
explained in the IPCC reports, the CO2 projections
would have been subject of critics since long.
Still I am puzzled about the extremely slow over all
ocean uptake whereas the C14 uptake was observed
to be more than 30 times faster. Note that both uptakes are considered
as being proprotional to the *delta* related to the
equilibrium concentration and I have not been confused about
anything. If you divide this delta by some quite constant quantity
and consider the ratio (in case of C14 the division was done by C12 which
only changes by some 7% within the considered time frame), that makes hardly
a difference. For C12-CO2 you would get the same response characteristics
and excess lifetime if you would calculate it for
the delta in permille related to 280 ppm for example. I hope, you
can find some basic explanation. I suppose the discrepancy has to do
with the Revelle factor that erroneously has been assumed not to apply
for C14. It cannot be caused by the slightly higher mass (4.5%) of
C14-CO2 molecules.
Best regards,
Peter Dietze
Re: Re Carbon Model Calculations (discussion..)
Tue, 08 May 2001 16:00:47 +0200
From: joos <joos@climate.unibe.ch> To: 091335371@t-online.de
CC: Enting <ige@dar.csiro.au>
Dear Colleagues,
The discussion on fitting procedures
and a two-box model is not fruitful. For anybody reasonably interested
in the carbon cycle I strongly suggest to read the literature. A good starting
point is the IPCC first, second and third assessement and the literature
cited therein.
Certainly, the carbon cycle is not
a linear electrical circuit. (Even if carbon cycle modeleres often
characterize the response of atmospheric CO2 to a perturbation using Green's
function.)
Here below two brief comments that may help to understand
what Mr. Dietze is doing. Frankly speaking Mr. Dietze
performs a pure curve fitting excercise that does not yield any reasonable
insight into the carbon cycle and the quality of carbon cycle models. A
waste of time. May be somebody else likes to explain the difference
between different impulse response experiments and between Delta-C14 and
14CO2 and so on.
Regards, Fortunat Joos
(A) Fitting a curve with two parameters (Reference:
mail from Mr. Dietze: 8 May 01)
The model used to fit the Bern-CC response is:
d/dt delta-CO2(atm)[ppm] = BF *
Emission[GtC/yr] /2.123 [GtC/ppm] -1/tau * delta-CO2(atm)
where delta-CO2 is the atmospheric CO2 increase in ppm
since preindustrial, tau is approximately 500 year and BF = 0.54
This means 46 % of emissions are
instantaneously removed in Mr. Dietze's fit. The decay term with
tau=500yr
is numerically not very important and
tau is not an indication of the life time of a CO2
perturbation in the atmosphere. I have no idea how
Mr. Dietze can claim that this is the lifetime
of the Bern CC model for a CO2 perturbation. Finally, to match the
curves better Mr. Dietze adjusted the preindustrial CO2 concentration for
individual fits.
(B) The 'All-RC-Model' (Reference: mail from Mr.
Dietze: 5 April 01)
The RC-model mailed earlier by Mr. Dietze corresponds
to a 4 box model with an atmosphere, two boxes of equal size as the atmosphere
which exchanges carbon with a rate of 1/10 yr (fast reservoir) and 1/3209
yr (slow reservoir) and a reservoir of infinite size that exchanges with
the slow reservoir with 1/4995 yr. On a century time scale this 4-box model
corresponds simply to a two box model where the atmosphere and the other
box are of equal size and exchange with a rate 1/10yr. This simply means
that half of the emissions stays airborne and the rest is taken up by the
other box on a time scale of 10 years.
This has obviously little to do with the real ocean and
surface-to-deep mixing as documented by the observed tracer distributions
(radiocarbon, CFCs, carbon , carbon isotopes, oxygen, nutrients ..). It
has also little to do with the terrestrial biosphere. But anyway, the figure
of the electrical circuit with capacities and resistance attached to the
projections of Mr. Dietze shown in an earlier mail is certainly 'impressing'.
"P. Dietze" wrote:
> I append my Excel file, so you can check my calculations
for the Web discussion, using the Bern IPERT
> impulse response. Be aware that the German Excel version
uses a comma instead of the decimal dot.
~~~~~~~~~
Comments by Peter Dietze:
My "curve fitting exercise" was not meant to supply any
"insight" into the complex carbon sequestration process and its modelling.
Such an insight cannot be obtained from the Bern model responses either.
No matter how sophisticated the Bern model internally is and thus how frustrating
my findings may be for the modellers - my cmodcalc.htm paper revealed
that the Bern model responds (even for three most different scenarios IS92a,
SRES A1 and WRE550 until yr 2100 rsp. 2300) quite exactly as my simple
linear RC model with T=570 yr, BF=53% (left hand figure) and an infinite
deep sea sink capacity (which could be short-circuited and taken out).
The parameters are
C1 = 2.123
GtC/ppm (atmospheric excess buffer)
C2 = 1.89
GtC/ppm (fast aux buffer for BF=53%, C2 is 47% of C1+C2 or equivalent
to 89% of an additional atmosphere)
R1 = 142
ppm/GtC/a (R1*{C1+C2} yields T=570 yr)
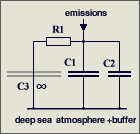
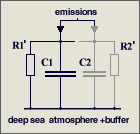
It is a misunderstanding that
47 % of the emissions are instantaneously removed
in my model differential equation. This equation copes with the
atmosphere alone (which takes 53%) and assumes that the aux buffer (which
takes 47%) and its discharge is in parallel but separated,
and C2*R2' = C1*R1'
= 570 yr (right hand figure), so that it can be split off and disregarded
because its response is identical to that of the atmosphere.
I do not at all agree to Dr. Joos' statement "The decay
term with
tau=500yr is numerically not very important
and tau is not an indication of the life time of a CO2 perturbation
in the atmosphere". The T (or tau) parameter is most
essential as it indicates how long it takes until an increment in
CO2 concentration, caused by an emission impulse, will take to be reduced
to 1/e or 37%. Moreover the sink flux is given
by excess_buffer_content/T. Of course such a lifetime approach is not used
in the Bern model, but as it responds in the same way, it
could approximately be replaced by this RC equivalent. Contrary
to Dr. Joos' impression, this simple RC model even
(roughly) comprises the response of the bisophere (as observed,
using T=55 yr and BF=75%) or as calculated within the Bern model (using
T=570 yr and BF=53%).
RE: Re Carbon Model Calculations (discussion..)
Wed, 9 May 2001 14:58:34 +1000
From: "Enting, Ian" <ian.enting@dar.csiro.au>
To: "P.Dietze" <091335371@t-online.de>
Just a few quick points:
1. The carbon cycle behaves non-linearly - the linear
apporixmations are only valid for relatively small perturbations. That
is why there are different responses listed in TP31.
2. The main cause of this non-linearity is well-established
(in some aspects for almost 100 years) ocean chemistry.
3. Neglect of this non-linearity seems
to be the main reason why Jarl
Ahlbeck's projections end up about 100 ppm or more lower than those
quoted by the IPCC.
4. As I said in my previous e-mail, the easiest way to
deal with the non-linearity is to model the air-sea exchange explicitly
and then define response functions for how the mixed layer responds to
a carbon perturbation. A linear approximation will have a much greater
domain of validity if you do this. Joos and coworkers have published response
functions that characterise the Bern model in this way so you will
have a basis for comparison with his results.
5. The non-linearity means that the limiting
carbon content M(lim) increases with the total emissions E(tot) faster
than linear. Because the Bern model responses are for small
perturbations, the 0.29 'remant factor' corresponds to dM(lim)/dE(tot)
and NOT M(lim)/E(tot). Even a small non-linearity can make these
quantities quite different.
6. Once you have multiple exponentials,
you can define a 'time-scale' in an infinite number
of ways. A definition of 'lifetime' will only apply for a
particular context. It is for this reason that when we wrote the carbon
cycle chapter for the IPCC radiative forcing report, we
avoided using the term lifetime in connection with CO2.
~~~~~~~~~
Comments by Peter Dietze:
Though the "All-RC-Model" is linear (because of its linear
differential equations), it can quite exactly model
the total response of the Bern model. The fact that the ocean's
uptake reduces with increasing charge, is modelled with an ocean
capacitor of limited size. Regarding the remanent fraction, there
is no difference between dM(lim)/dE(tot) and M(lim)/E(tot)
in my model, i.e. the remanent fraction is independent from the charge.
This would not hold for a saturated ocean, but we should be aware that
this question is only of theoretical value because the ocean is not at
all well mixed and as long as fossil fuels are available (and even several
centuries therafter), plenty of "non-Revelled"
water from the deep see will be upwelling.
Moreover the water of the upper layer, moving towards the high-altitude
downwelling areas, becomes icy cold so that
any assumption, the CO2 uptake will essentially be limited by Revelle,
deems rather unrealistic.
Regarding multiple
impulse response exponentials, the choice
of a resulting or effective time constant T (for
the time range of fossil fuel use which the model is applied for)
is only possible in a small range (depending on the chosen buffer fraction
BF), as my curve fitting revealed. What counts here (contrary to a short-term
response calculation), is only the combination of the fraction with T=infinite
(remanent fraction)
and the next largest time constant (e.g. 507
yr). The contributions with smaller time constants
(e.g. 16.5 yr and 3.5 yr as in CSIRO TP 31, p.38 for IPERT) soon
vanish to zero. The choice of one time constant
is indeed a good and practical approximation. But 570 or 480 years as been
found by curve fitting, seems absolutely unrealistic
- apart from strongly contradicting the ~120
years always being quoted by IPCC people without
knowing from where it originates.
Answers to questions, finally
Fri, 18 May 2001 16:49:51 -0400
From: harvey@cirque.geog.utoronto.ca To: p_dietze@t-online.de
Dear Peter:
Sorry to take so long in replying to your email of April
23rd. I have not had a chance to look at your carbon cycle model, but I
can answer your basic questions: (1) why is the equilibrium time between
surface water and air about ten times longer for 14C than for total carbon,
(2) why is the atmospheric lifespan of C isotopes so much shorter than
that for total C, (3) how can these two statements be reconciled with each
other, and (4) why it is not appropriate to think of the oceanic uptake
of carbon in terms of a single time constant?
The behaviour of carbon in the ocean is quite complicated
and the literature is not very clear, so it is not at all surprising that
you have these persistent questions. I've only pieced it together by asking
lots of face-to-face questions over a period of time, being tipped off
on some key papers published in the 1970's that actually explained what
they were talking about (one by Broecker in particular around 1974), and
then doing various back-of-the-envelope calculations that illustrate the
key factors (these calculations I used in my book). Everything that
I explain below is also discussed in my book (which is why I referred you
to it the first time), although not in a way that explicitly addresses
question (3).
First, here is some key information that eventually ties
the answers to all these questions together: dissolved inorganic carbon
(DIC) in the ocean occurs in three forms: as dissolved CO2 (about 0.5%
in the surface mixed layer), CO3 2- (about 12%), and as HCO3-
(about 87.5%). Through a series of chemical reactions, carbon continuously
changes between these three forms. The partial pressure of CO2 in the mixed
layer ((pCO2)ml) depends on the concentration of CO2, not of DIC. Similarly,
the partial pressure of a given isotope depends on the concentration of
CO2 for that isotope, not of DIC. CO2 (or a given isotope) will flow from
the atmosphere to the mixed layer if the atmospheric pCO2 (or isotopic
pCO2) is greater than the mixed layer pCO2, and vice versa. This also applies
to individual isotopes.
The reactions that occur when CO2 is added to the mixed
layer are:
CO2(gas) + H2O(liquid) (r) H2CO3(aq)
(1)
H2CO3 (r) H+ + HCO3-
(2)
CO32- + H+ (r) HCO3-
(3)
giving the net reaction:
H2O + CO2 + CO3 2- (r) 2HCO3-
(4)
Of course, the reverse of all these reactions also occurs,
and eventually a new chemical equilibrium is established with forward and
reverse reactions occurring with equal intensity. There are two critical
facts about the resulting new equilibrium:
First, the added CO2 does not distribute itself
among the three forms of DIC in the same proportion as the pre-existing
carbon. Rather, the added CO2 remains disproportionately in the form of
dissolved CO2, such that the relative concentration of CO2 increases about
9-10 times faster than that of DIC. That is, if enough CO2 is added to
increase DIC by 1%, the CO2 concentration (and hence pCO2) will increase
by 10%. This factor of nine or ten is referred to as the "buffer factor".
Second, as CO2 enters ocean water, the CO3 2- concentration decreases
due to the fact that it is consumed by the net reaction shown above.
The final point is that, as your chemical colleague pointed
out, there is no difference in the chemical behaviour of any of the carbon
isotopes. This, rather than being a reason for expecting the same atmospheric
lifespan for the different isotopes (as you inferred) is actually part
of the reason why the atmospheric lifespans are so different!
Now to your specific questions.
Why is the adjustment time for isotopes about 10 times
slower than for total C?
Consider an isolated system consisting of only an atmosphere
and mixed layer box, and suppose that we add 200 molecules of CO2 to the
atmosphere, all as 14CO2, and ignore 13C for simplicity. These molecules
will distribute themselves among the three forms of DIC in the same proportion
as the pre-existing DIC (i.e.: only 0.5%, or 1 molecule, as 14CO2).
Thus, the back pressure of 14CO2 hardly changes at all. However,
the perturbation in total carbon distributes itself as required by the
chemical equilibria (i.e.: as 10 molecules as CO2, 9 of which will be 12CO2).
Thus, the mixed layer pCO2 for 12CO2 rises, even though no 12CO2 was added
to the mixed layer. What is happening is that, when a 14CO2 molecule enters
the mixed layer, reaction (3) occurs and it ends up as H14CO3 -. However,
when the reverse of reaction (3) occurs, it is exceedingly likely to involve
one of the pre-existing HCO3- ions, which are overwhelmingly H12CO3 -.
It is because there is no chemical difference between 12C and 14C that
this occurs and, as you will see, this leads to the answer to your first
question.
The rapid rise in the back pressure for total C effectively
reduces the size of the available mixed layer reservoir, and this smaller
effective reservoir sizes causes the adjustment time to be smaller for
total C than for 14C. This can be seen if we write down the linearized
differential equations governing the change in the perturbation of atmospheric
and mixed layer carbon as a result of flow between the mixed layer and
atmosphere. For total carbon, these equations are:
d(DCa)/dt = k'( bDCml-Ca)
(1)
and
d(DCml)/dt = -k'(bDCml-Ca)
(2)
where b is the buffer factor
and 1/k' is the turnover time t. The exponential
time scale for the adjustment time, that arises from the solution of these
differential equations, is
tadj = 1/(k'(1+b))
= t/(1+b)
(3)
For 14C, there is no b
factor, so you can see that the time scale for the atmosphere and mixed
layer to come into equilibrium with each other is about 10 times faster
for total carbon than for a 14C. Also, by analogy with an equation of the
form
R d(DCa)/dt = aDCml
(4)
where R is a reservoir volume and aDCml
is a mass flux, you can see that a larger constant term on the RHS of equations
(1) and (2) has the same effect as making the reservoir size R smaller
in eq. (4).
Why is the decay in the atmospheric impulse response
for isotopes much faster than for total C?
The above analysis explains why the atmosphere and mixed
layer approach the steady state distribution of total C about 10 times
faster than they approach the steady state distribution of isotopic carbon,
following a pulse input to the atmosphere.
However, those steady state distributions are quite different
for isotopes and for total carbon.
Again, consider a system consisting of an atmosphere and
a mixed layer, initially with equal amounts of C and a buffer factor of
9 (this is a very good approximation to reality). The steady state distribution
of a pulse of carbon between the atmosphere and mixed layer will be such
that the increases in pCO2 for the atmosphere and mixed layer are equal.
Since mixed layer pCO2 rises about 9 times faster than that of the atmosphere
(due to the buffer factor), the carbon content of the mixed layer needs
to increase only 1/9 as much. Thus, about 90% of the carbon will remain
in the atmosphere, and only 10% will go into the mixed layer. Of course,
nature contains a deep ocean underneath the mixed layer, and excess carbon
gradually diffuses downward, allow more carbon to be taken up by the mixed
layer. However, the downward diffusion is a slow processes - it serves
as the bottleneck in the oceanic uptake of anthropogenic CO2, giving a
rather slow atmospheric impulse response.
In the case of 14C, however, the steady state distribution
- even with a mixed layer only - sees almost all of the carbon going into
the mixed layer, and almost none remaining in the atmosphere. This is because
of the processes that I explained in the discussion of 200 molecules. Thus,
even though the time scale for the atmosphere and mixed layer to reach
their own steady state is 10 times longer for 14C than for total C, they
are heading toward much different equilibrium partitionings of the injected
C. Thus, the perturbation in atmospheric 14C initially falls much more
rapidly than the perturbation in total C in the atmosphere (this is illustrated
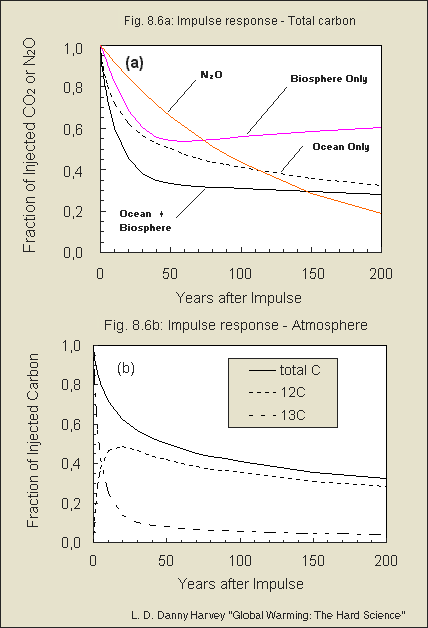
in Fig. 8.6 of my book).
Note that the answer to neither
of the above questions involves the marine biosphere.
Why is the oceanic uptake of C not governed by a single
time constant?
The oceanic uptake of carbon is governed by a succession
of distinct processes, each of which has there own time constants. The
step is atmosphere-mixed layer exchange, which has a time constant of about
1 year. Next, is downward diffusion, which proceeds slowly and involves
a progressively deeper part of the ocean. Then there are feedbacks involving
mixed layer temperature (and possible changes in the biological pump induced
by changes in ocean circulation). All of these processes eventually allow
the ocean to take up about 85% of the C that humans could ever inject into
the atmosphere by burning fossil fuels on a time scale of about 1000 years.
As the ocean absorbs C, the CO3 2- concentration falls. This induces dissolution
of carbonate sediments, replenishing some of the CO3 2- in the adjacent
bottom water. As this water circulates back to the surface, more CO2 can
be absorbed by the atmosphere. Eventually, another 10% of the injected
carbon can be absorbed - but on a time scale of many thousands of years.
So - because of the variety of processes involved in the
oceanic uptake of C, it cannot be characterized by a single time constant.
This, and the behavior of the isotopes, is illustrated in Fig. 8.6
of my book, which I am including as a separate attachment. The figure shows
the impulse response for N2O, which has a time constant of 120 years. The
decay of the CO2 pulse in the atmosphere is initially much faster than
this, but later is much slower than this.
This should answer your questions. I
have two papers recently accepted by JGR-Oceans that present a new,
quasi-1D coupled climate-carbon cycle model that I can send you if you
are interested. The papers have the complete set
of equations needed, and the result is the behavior discussed above.
Also, I will be submitting a paper next week to JGR-Atmospheres
entitled "Understanding the Transient Response of Coupled Climate-Carbon
Cycle Models to Changes in Ocean Circulation and Mixed Layer Warming",
which I can also send you if you're interested.
Yours truly,
Danny
Re: Carbon Model - contribution of Dr. Harvey
Sat, 19 May 2001 21:47:00 +0300
From: jarl.ahlbeck@abo.fi To: 091335371@t-online.de>
Hello Peter,
A comment on the letter from Dr. Harvey that you are free
to forward to anybody. Comment based on 30 years experience as chemical
engineering process modeler.
- Let's start from the backmix approach, atmosphere and
surface layer water in equilibrium. A static situation, no dynamics involved.
- The chemistry Dr. Harvey described is over-simplified,
click for a more complete description:
http://www.john-daly.com/oceanco2/oceanco2.htm
- In fact, the solution of the ocean water equilibrium
chemical equation is far from trivial, please contact Prof. Tapio Westerlund
<tapio.westerlund@abo.fi> for details. I have not yet seen any other
complete solution of the static batch-problem than the computer simulation
program made by Westerlund. The batch is extremely well mixed, 200 GtC
going up and down every year and good mixing of the ocean surface layer.
When considering this back-mix situation only, the airborne
fraction and the absorbed fraction of an emission is always constant (time
delay 8 months or so). When putting additional carbon into the system,
a new fast equilibrium is achieved with more carbon in both the atmosphere
and in the surface water. Part of the new carbon in the atmosphere originates
from old CO3-- and HCO3- ions in the water that degasses up in the air
as CO2 when the pH decreases.
If there is a tracer in the emitted carbon, it
will appear to be absorbed to a greater extent than the other emitted molecules,
because part of the "new" CO2 in the atmosphere is in fact old CO2 from
CO3-- and HCO3- thus diluting the tracer concentration
in the atmosphere. If all emitted molecules could be labeled, you will
find very little of them in the atmosphere after some months, much
less than the total increase of CO2 molecules in the atmosphere.
Taking only the static situation into account, there is
a constant airborne fraction of emissions staying in the atmosphere (forever)
and no life time can be calculated. A life time
for C-14 is not relevant at all if you want to say something
about the absorption of anthropogenic carbon.
Now taking dynamics into account, the only dynamics that
counts in a Greenhouse discussion is the mass transport
from the surface layer down to the deep layer. This is said to be
very slow, a second order Fick's diffusion. Here the C-14 comes in as ocean-C-14
has been used in the Bern model (as far as I have understood) to calculate
the diffusion constants for the Fick's second order differential equation.
The Bern model contains a minor diffusional component too. But these constants
have been calculated at a different situation as today with less carbon
in the system which make the relevance of the obtained constants highly
questionable. Mass transport from the surface water to "virgin" water means
that the airborne fraction is no more constant. If you have small emissions
enough, you will have zero airborne fraction (or even negative as carbon
disappears from the atmosphere), for big emissions you will get small airborne
fraction. The airborne fraction will change with time and atm concentration.
I think the important mass transport from the surface
to the deep water is poorly understood and not even
necessarily structured according to the Fick's second order. There
are many simultaneous mechanisms going on, not only steady-state diffusion,
but also influence from surface water currents streaming down and causing
direct first-order diffusional contact to "virgin" water. Westerlund
uses an "equivalent surface layer thickness" that is a function of the
time (increases as times goes by).
If the diffusion is controlled by
a first order Fick's equation to a greater extent than by the second order,
the absorption rate is almost directly proportional
to C(surf.carbon)-C(deep layer carbon) or to C(atm)-280 ppm. The
rate constant may calculated statistically from available data. The problem
is the intercorrelation between emissions and concentration making an idealized
batch describing recent data almost as well (constant airborne fraction)
as when taking significant mass transfer to deeper layer into account (variable
airborne fraction). I have walked around the problem by calculating the
airborne fraction from data although I do not like this parameter, it feels
a little unscientific.
The decrease of the airborne fraction
from close to 80% in the 1960:s to 39% today (deforestation included
in the emissions) point towards a strong diffusion mechanism in the ocean.
It may be of first order, or second order with high diffusion constants.
If this is not the fact (nobody knows the real truth), the
biosphere is to blame (both land and ocean biotics) for
over-reacting to increased carbon concentration.
I prefer not to talk about lifetime
of anthropogenic carbon in the atmosphere at all. It may trivialize a very
complex problem. My statistical mass-transfer model, however, based
on Fick's first law of diffusion, is structured
in the same way as Peter's model, both agree very well with observations
and give lower future concentrations than IPCC/Bern for emissions IS92a.
The Bern model applied on IS92a implies abt. 50% airborne fraction when
today's number is already down to 39%.
Cheers, Jarl
P.S.: Atm. CO2 increase during 2000 for Jubany Station,
Antarctia (Luigi Cattaglia at the CDIAC site) was only ** 1.04 ppm ** [airborne
fraction: 25% P.D.]. The mean value
1994-2000 was 1.7 ppm/yr, quite high due to the strong influence of warm
1998 El Nino, with a 2.14 ppm increase for 1998. The year 2000 was La Nina
- cold, thus moving the equilibrium ocean surface water/atmosphere towards
more carbon in the ocean surface. Do you remember when the doubling of
CO2 should occur ?
Re: Carbon Model - contribution of Dr. Harvey
Sun, 20 May 2001 09:49:51 +0200
From: "P. Dietze" <091335371@t-online.de> To: jarl.ahlbeck@abo.fi
Dear Jarl,
thanks very much for your contribution that I just had
a first glance. As you are a chemist you, too, seem not very fond of lifetime
considerations. But you should be aware that - supposed the sink
flow is indeed roughly proportinal to the partial pressure increment exceeding
the equilibrium - the sink flow is excess_buffer_content/T. If the
carbon excess of the atmosphere + aux buffer is given, and
T is somewhat arbitrary, the sink flow would be arbitrary (!) and
this seems why IPCC insists to be right in projecting any future accumulation
and to keep undisputed.
Btw, in an interwiew Guy Brasseur (now MPIM director)
said, if we would aim to stabilize the present 370
ppm, we would have to reduce the global CO2 emissions to 10%. If
you enter my "Bern simulation" parameters T=570 and BF=53% to my stabilization
formula below Fig.7 of my cmodcalc.htm paper, you get that 10% emission
E=0.63 GtC/yr !!!!
My main problem is that you have so far not solved for
my most essential point: did IPCC possibly apply the Revelle factor twice
as they assumed it does not apply for C14? Or is their eddy diffusion approach
so far away from reality (including biomass) that
it accidentally makes a factor ten smaller sink flow?
You are right that neither the airborne fraction (see
my Fig.2) nor the C14 lifetime of 16 yr is so essential, as
any individually tagged CO2 molecules vanish faster (by turnover
and intermixing) because those which return are mostly
untagged. But can it be that the lifetime difference makes a factor
of 35 ??? Jarl, these questions are MOST ESSENTIAL...
Best regards,
Peter
Carbon Model - contribution of Dr. Harvey
Mon, 21 May 2001 10:32:18 +0300
From: "Jarl Ahlbeck" <jarl.ahlbeck@abo.fi> To: <091335371@t-online.de>
Hello Peter,
It is difficult to say very much about the eddy diffusion
approach by the IPCC, other than it statistically seems to give a too small
absorption rate. From a statistical point of view, it is impossible to
say if the observed partial-pressure forced high absorption rate is due
to the biosphere or to the ocean water.
The IPCC ocean chemistry including the Revelle factor
is strange and I must admit that I do not understand
how they can handle the problem without a complete computerized treatment
of the backmixed surface layer chemistry including the charge balance,
the pH solving that is far from trivial, and the numerous chemical equilibrium
constants.
But C-14 can be considered as a tracer (in mixers you
may use tracers to measure the degree of mixing) that
has only indirectly anything to do with the partial-pressure forced absorption
of anthropogenic carbon. In the ideal back-mixed system atmosphere-surface
water a C-14 impulse will immediately be split into two parts, atmosphere
and mixed water. If there would be no mass transport out of the system,
the C-14 in the atmosphere would rapidly decrease to a level corresponding
to the part of total carbon that is normally located in the atmosphere
and stay constant after that. If the C-14 anyway starts to decrease in
the long run, and we consider the surface-atmosphere batch only, it may
be due only to two mechanisms:
- Process 1: Replacement of atm CO2 molecules by degassed
HCO3- and CO3-- due to (anthropogenic) pH decrease, not modelled by the
IPCC as far as I understand. If there is no decrease of pH, or no anthropogenic
emissions, Process 1 does not happen at all, the pH is constant, and the
C-14 content of the atmosphere remains constant after the initial fast
split.
- Process 1a: Dilution of total carbon in the backmixed
system by anthropogenic emissions, not very important.
- Process 2: Diffusion to "virgin" water outside the batch.
Or to the biosphere.
Process 2 occurs very slowly in the pre-industrial situation
as
it is mainly slow mixing/diffusion and no partial pressure forced diffusion,
but accelerates as the the system goes out of balance
due to anthropogenic emissions, with large driving concentration
difference between surface water currents and "virgin" water. The difference
between C-14 in the atmosphere, say between 1990 and 2000 may be used as
a measure of this diffusion process if corrected for Process 1, just like
any industrial tracer would have been used.
A corrected calculated lifetime of old atmopsheric C-14
obtained from the decrease rate say 1990-2000 would, if you want, be
about the same as the lifetime for atmospheric carbon during the same period.
Correspondingly, in future, going up to say 500 ppm, the process will go
faster.
Imagine that you have 500 ppm in the atmosphere at the
year 2050 and all emissions are stopped. Nature will continue to suck carbon
dioxide from the atmosphere at a high rate due to the high partial pressure.
Then you put in an impulse of only 0.5 GtC anthropogenic carbon. It will
be fastly divided between atmosphere and water and
then start to disappear, not because of the small additional imbalance
it produces, but because of the general non-equilibrium situation.
The same will happen with an impulse of 100 molecules C-14 that
do not produce any additional partial pressure imbalance either.
Cheers, Jarl
...well, that may not help much, but its is the way a
chemical process engineer would treat the problem.
Re: Carbon Model - contribution of Dr. Harvey
Mon, 21 May 2001 13:05:22 +0200
From: "P. Dietze" <091335371@t-online.de> To: jarl.ahlbeck@abo.fi
Dear Jarl,
thanks for your response. It is indeed very difficult
to understand IPCC's Revelle approach as they seem to comprise it in the
response of (even small) impulses, considering boundary layer effects,
but except C14 - whereas I consider Revelle more
under static or short term (mixed layer) and long term (all ocean) aspects.
Moreover the downwelling icy cold water and the upwelling "fresh" water,
not
being subject to Revelle, IPCC seems not to cope with.
Re you, I now have the impression that you have not really
understood the characteristics of a *linear system* and thus my CO2 lifetime
approach - not to mention that of C14 with its very small 10^-12 fraction.
Any
additional CO2 impulse - no matter how small and whether tagged or not
- can NOT be considered as to be taken away with the main stream!! [As
long as we consider CO2 concentration, but not intermixing and thus disappearing
of individually tagged C14 molecules]
it ONLY obeys to the individual increment in partial pressure - and the
1/e lifetime is constant for any fraction and INDEPENDENT of the main
disequilibrium flux (which btw obeys to the same characteristics). I clearly
said that for a linear system every perturbation can be superposed *additionally*
and gives just an *additional* response which has no cross-interference.
Suppose you speak to your wife at the phone (an almost
linear transmission system). Inbetween you hear a dog barking and then
a baby crying. The voice of your wife is uneffected by the dog and the
baby - you hear all together *additionally* and uneffected in volume and
by each other. If your wife whispers, you hear her whispering - even if
the dog barks loud, her voice is not boosted.
The same holds for a tiny C14 impulse within the huge
CO2 exchange - believe me as a control engineer or not. I feel, IPCC tries
to cope with Revelle around the boundary (elementary diffusion and chemical
equilibrium), thus introducing their nonlinearity - and making the matter
worse below by using (gradient controlled!!) eddy diffusion. Of course,
my linear approach can be disputed. It may be wrong for the very first
time interval, but if we consider 10-50 years of the uptake process, we
globally have a vast intermixing and (as you found) mostly
a linear uptake proportional to the partial pressure increment.
So I am still left with my question whether IPCC might
have applied Revelle twice - and what they have done and imagined at all
[and possibly leaving out the strong impact of temperature on chemical
equilibrium]. It is not easy to properly interprete Harvey's equations
and their differential equation solution.
Best regards, Peter
Lifetime of any CO2 impulse, statistically obtained
Tue, 22 May 2001 15:27:56 +0300
From: "Jarl Ahlbeck" <jarl.ahlbeck@abo.fi> To: <091335371@t-online.de>
Dear Peter,
You are right, my thoughts have been a little locked on
the static chemistry and on explanation (statistically) of the "bulk" sink
flow. Of course a delta m impulse emission, causing a delta C impulse of
atm concentration driving difference will give an
impulse response and behave in the same way regardless of the bulk flow
and regardless of the size of the impulse. (I read only a basic
course in process control/process dynamics and all my industrial modelings
have been steady-state modeling with mean flows). So you are quite right,
and I tried to see what first-order (linear) system lifetime would come
out of my regression coefficients:
Statistical sink flow eq. was Fsink = 0.0561(C-275.5)
or dC/dt = -0.0264(C-275.5), both 0.056 and 275.5 (as pre-industrial level)
are regression coefficients. Half-life time of any CO2 impulse correspondingly:
T(1/2)=ln(2)/0.0264 years = 26.26 years.
Does it make sense? Numbers based on regression coefficients
only, no "own opinions" are involved. All emission/concentration data from
the best available sources 1970-1999.
Cheers, Jarl
~~~~~~~~~
Comments by Peter Dietze:
Based on Jarl's statistical analysis, the 1/e excess CO2
lifetime is 1/0.0264 = 37.9 years. For example, if we take a (smoothed)
concentration of 364 ppm and 8.1 GtC total emissions for 1997, Jarl's sink
flow is 0.0561*(364 - 275.5)
= 4.96 GtC/yr. This is obviously best-fit estimated from an (observable)
airborne fraction of 39% as the sink flow seems to be 8.1*(1
- 0,39) = 4.96 Gt C/yr.
But these calculations do not cope
with the existing fast auxiliary buffer. If we assume 25% of the
atmosphere, the real sink flow is only 8.1*(1
- 0,39*1.25) = 4.15 Gt C/yr.
The difference of 4.96 - 4.15 = 0.81 GtC/yr, which is not sequestered,
goes
into the auxiliary buffer. With the total excess buffer content,
divided by the real sink flow, we get a lifetime
of 1.25*(364
- 275.5)*2.123/4.15 = 56.6 yr.
I suppose, a new regression analysis, coping with the auxiliary buffer
(I estimated 33%), will yield correct results.
Re Answers to questions, finally
Thu, 24 May 2001 16:12:53 +0200
From: "P. Dietze" <091335371@t-online.de> To: harvey@geog.utoronto.ca
Dear Danny,
sorry, I had a lot of trouble with my computer these days,
so my response and thanks re your elaborate mail from last Friday got quite
late. Inbetween I tried to discuss the matter with three chemo-physicists.
One said, you are right, one said you are wrong - and the other even found
a CO2 time-constant (backed so far by an unchecked statistical regression
analysis) about 33% less than my 55 yr.
So I have not yet come to a proper conclusion and so long
I will wait before I put your formulas and my answer onto the Website.
Your conviction that in case of a C14 excess *all*
dissolved C of the mixed layer will take part in the exchange (and
even make it much faster) - but in case of a C12
excess only the amount of dissolved C, divided by a Revelle factor of about
9 - so far deems quite unrealistic to me. Suppose, the C14 is
nothing but a labelled C12... and chemically
behaves mostly like C12 as well.
Thank you for the xls file, but my (German) Excel '97
aborts when I try to open it. Re the excess CO2 impulse lifetime you may
be right in some respect. In the very first beginning the uptake may be
fast indeed. And for the last tail, considering sedimentation within some
millenium, it is indeed very slow. But you seem not to realize that I calculated
the bulk uptake characteristics from sink flow observations (i.e.
accumulation vs. total emission) of the last century. This yields effective
(or apparent) 55 years. And with my "curve fiitting"
and a single 570 yr lifetime I was able to perfectly fit the Bern model's
response from preindustrial to 2100 - and even up to 2300 for WRE 550.
So the Bern lifetime *is* practically 570 years, no matter what functions
the Bern model is using internally.
Recently I read about MPIM director Guy Brasseur. He said,
if
we would aim to stabilize the present 370 ppm, we would have to reduce
global CO2 emissions to 10%. If you enter 370 ppm, T=570 yr and
BF=0.53 into my stabilization formula below Fig.7 at http://www.john-daly.com/dietze/cmodcalc.htm
you
get 0.63 GtC/yr, just about 10% of the emissions
[with T=480
and BF=54% E would be 0.74 GtC/yr]. Isn't this another proof that my
finding is right?
Best regards,
Peter
P.S.: I forgot about your kind offer to send me your new
papers. I am mostly interested in the JGR-Oceans one with your new, quasi-1D
coupled climate-carbon cycle model and the equations. See my address below.
Please send me Fig. 8.6 of your book as well.
Peter Dietze's Paper - Review Comment
Tue, 29 May 2001 10:28:58 -1000
From: George and Teresa Birchard <gfb@aloha.net> To:
daly@john-daly.com
Dear Peter,
You wrote "Still I am puzzled about the extremely slow
over all ocean uptake whereas the C14 uptake was observed to be more than
30 times faster."
This result is not surprising if
the concentrations of CO2 in the surface layer are close to equilibrium
with atmospheric CO2 concentrations. Near equilibrium the forward
and back reactions of CO2 dissolution are occuring at the ocean surface.
These reactions tend to have little effect on carbon 12 and 13 which are
near equilibrium, but will tend to remove C-14 from
the atmosphere because it is enriched in the atmosphere by bomb testing
and therefore is way out of isotopic equilibrium.
The processes that transfer carbon from the surface ocean
to the deep ocean occur at a slower rate than the air water exchange of
CO2. Thus you are comparing different processes - apples and oranges -
when you compare C-14 isotope exchange with deep ocean uptake of CO2.
Regards,
George Birchard
~~~~~~~~~~~~~
Comments by Peter Dietze:
As can be seen in my mail to Jarl Ahlbeck on 21 May, the
lifetime
of a C14 impulse - if only the bulk atm. CO2 concentration is considered
- should be based on cross-interference-free linear uptake and thus be
independent
from i) the size of the C14 impulse and ii) the C12 disequilibrium and
associated sink flux of the present perturbation of the global carbon
cycle. The C14 uptake (which is not observable
by atmospheric measurements) should take place with practically the same
sequestration time constant as for C12. The over three times faster than
55 yr disappearance of the bomb C14 is not
caused by sequestration, but just by fast intermixing with the ocean
boundary and mixed layer which can be considered as an auxiliary buffer
connected to the atmosphere (but delayed). Nearly all what is returned
to the atmosphere during intermixing (before sequestration takes over),
is C12-C02 which thus only dilutes the C14-CO2 impulse.
We can be sure there is no separate chemical disequilibrium
and sequestration lifetime for isotopes as the GEOSECS Fig. 8 in my
cmodcalc.htm paper and my red and green triangle indicating a "disappearing
lifetime" of 16 years may suggest.
IPCC science and the Prof. Mörner problem
Sat, 2 Jun 2001 10:36:57 +0300
From: jarl.ahlbeck@abo.fi
Dear all, a comment about the scientific level of IPCC/TAR:
On May 16th, on a seminar in Stockholm, an ocean researcher
said about the sea level chapter in IPCC/TAR: "Most of the recent high-quality
oceanic science has not been taken into account at all. If the way of treating
science in the rest of the chapters follows the same principles, the whole
report is worthless".
Unfortunately I would say the same
about the carbon dioxide circulation chapter. For the inorganic
gas (CO2 is not the only gas) chemistry in multiple salt solutions the
problem is that the best knowledge is concentrated on a few specialized
persons in the world that have published either in a few very specialized
chemical journals (for example Chemical Engineering Science) or in internal
university reports. The information may be a company secret or hidden into
computer programs and databases. These scientists are not involved in GW
research at all. The information is not available or even known by "global
carbon dioxide circulation modelers" who replace complicated chemistry
with som trivial "Revelle-factor-equations" and have no ability at all
to model the temperature dependent equilibrium mechanism correctly. The
calculation of this mechanism involves the management of 20 equations consisting
of acid-base expressions, dissolution expression, mass balances, charge
balances, expressions for the temperature dependence of all constants,
and a numerical solution of pH that is far from trivial [not to mention
the behaviour of individual isotopes P.D.]. And we still talk only
about a simple back-mixed batch with no kinetics or biological activity
involved!
I do like to hear how a IPCC-carbon dioxide modeler explains
the low increase of 1.04-1.3 ppm CO2 in the atmosphere last year!...
Cheers, Jarl
Carbon dioxide in SPM and TS
Thu, 7 Jun 2001 11:14:00 +0300
From: jarl.ahlbeck@abo.fi> To: mmaccrac@usgcrp.gov, rcourtne@uk.packardbell.org,
timo.hameranta@pp.inet.fi>, dwojick@shentel.net>, "Stott, Philip" <stott2@compuserve.com>,
...
Now I have nice new printouts of both SPM and TS [final
versions of the IPCC WG Reports Technical Summaries are available at http://www.ipcc.ch/].
Of course, I first looked up what was written about the CO2 cycle, because
I have done some statistical calculations on the subject myself. In SPM,
page 12/20 it is written. "As the CO2 concentration of the atmosphere increases,
ocean and land will take up a decreasing fraction of anthropogenic
emissions".
Then I opened my fresh printout of TS. On page 19/20 there
is a table:
-----------------------------------------------------
GtC/yr
1980-1989 1990-1999
atm incr.
3.3 +- 0.1 3.2 +-0.1
emissions
5.4 +-0.3 6.3 +-0.4
-----------------------------------------------------
These numbers in the TS give an uptake of 39% of
emissions in the 1980:s and an uptake of 49% in the 1990:s, a statistically
significant increasing uptake fraction. Still IPCC claims in the
SPM that we will have a decreasing uptake fraction
in the future. Is this the only bluff in the SPM?
Cheers, Jarl
Comment by Peter Dietze in an email distributed on
Thu, 07 Jun 2001:
I think, I have now solved the puzzle of the fast C14
uptake (GEOSECS Fig.8 at www.john-daly.com/dietze/cmodcalc.htm). See my
answers to Dr. Ahlbeck and my comments for George Birchard (29 May).
Bomb radiocarbon C14 is of course subject to the Revelle
factor for *all* dissolved carbon in the ocean in the same way as C12 (!),
and the C14 sequestration has to take place with the same time constant
as C12. The C14 isotope chemically behaves quite in the same way as C12.
The apparent fast initial *disappearance* (with T=16 yr) must be caused
by intermixing (turnover-exchange) with the upper ocean layer (my auxiliary
buffer) and should not be misinterpreted as *uptake*.
It is not at all likely that the C14 uptake is over 30
times faster than C12 because the Revelle factor does not apply (as assumed
by IPCC modellers). The initial C14 uptake dynamic seems not to be useful
for modelling the C12 sequestration - to which the Bern model has practically
allocated a time constant of about 500 years, which is (according to my
findings) an order of magnitude too high.
Your publications, book & carbon lifetime
Mon, 11 Jun 2001 13:33:36 +0200
From: "P. Dietze" <091335371@t-online.de> To: harvey@cirque.geog.utoronto.ca
CC: joos@climate.unibe.ch, Jan.Goudriaan@pp.dpw.wau.nl,
jarl.ahlbeck@abo.fi, bconeill@brown.edu, Enting <ige@dar.csiro.au>,
wigley@meeker.ucar.edu, broecker@ldeo.columbia.edu, Robinson <art@oism.org>,
singer@sepp.org, jaworo@clor.waw.pl, t.v.segalstad@toyen.uio.no, Hartwig.Volz@rwedea.de,
lars@internetami.se, daly@john-daly.com
Dear Danny,
thank you a lot for sending your two submitted papers
for JGR-Atmospheres "Understanding the Transient Response..." and for Journal
of Climate "Simultaneously Constraining..". I had a first glance and was
very impressed about the lot of highly sophisticated and professional work
you have done. As the stuff is quite complicated, I'll take some time to
analyze it. You said, you'll send me the two other papers as well that
you prepared for JGR-Oceans.
Special thanks for sending me pp.179 and 182 of your book
"Global Warming: The Hard Science". This text book seems to properly explain
the matters and is really what I would be interested in. I tried amazon.com,
it is there, but out of print. Only second hand copies can be ordered (if
somebody is willing to sell his)..
Fig. 8.6 b is excellent - the curves
really clear up the puzzle of the very fast isotope "uptake" by just intermixing/exchange
with the mixed upper ocean layer - thus setting free an adequate amount
of C-12. Then both together are sequestered just similar to normal C-12
!!!
As I already indicated in my updated Web discussion, this
process may have little to do with the Revelle factor - and an
isotope should as well be subject to the *total C* Revelle factor.
This contradicts your statement (on 18 May, as I understood it) that
C-14 is not subject to Revelle and thus disappears ten times faster
and within short time to "almost none" in the atmosphere. You assumed,
the
mixed layer has roughly about the same total C as the atmosphere
and about 1/9 of that amount if Revelle is applied - then
C-14 should fastly exchange to 50%. But of course, during this exchange
already the sequestration starts, reducing it bit more.
But what I am puzzled about in your
Fig. 8.6 (b) is that more C-12 is set free while the isotope intermixes,
than total C is left. To my opinion the curve of set free C-12 should
be less, so that the *addition* of the isotope and
C-12 is always equal the total C - right? Moreover I wonder why
in Fig. 8.6 (b) the decaying total C curve is less
than the "ocean only" in (a), but more than
"ocean+biosphere". Any explanation for that?
Re the problem of multiple exponentials
versus my good simple two parameter approximation, I think, I can offer
now a solution. My approximation (take
for example the Joos IPERT impulse response G(t) of Tab. 9.4 from CSIRO
TP 31, p. 38, see figure of my 8 May contribution), puts
together the fast decay terms (for T=3.05 and T=16.5 yr) to some 0.5 fraction
for the immediate [or fast] aux buffer. The other part (0.3
for T=infinite and the rest with T=507 yr) was taken together
for my T=570 yr. This makes little discrepancies if you consider
only 100 years of a fossil use scenario where a series of emission impulses
(say one per year or as in my case one every 5 yr) occurs and somehow the
addition
within the response mix levels out the differences that turn up
in comparison to the "correct" calculation with multiple exponentials.
By the way, the exponential T is
the average time an injected amount of CO2 stays in the air [the
partial pressure increment being considered]. With Excel I made a test
for a fancy impulse response function G(t) = 0.28 exp(-t/15) + 0.32 exp(-t/30)
+ 0.4 exp(-t/60), replacing it by a function with one
time constant only: (0.28 +0.32 +0.4) exp(-t/T) with T
= (0.28*15 +0.32*30 +0.4*60) /(0.28 +0.32 +0.4) = 38.7 yr
The curve that came out was hardly different. One reason
- apart from the time constants not being too far apart of each other -
is
that (because T is the mean resident time) the integral for t=0 to infinite
over the original exponential fractions is the same as the integral over
the replacement curve, i.e. 38.7.
I think I have found out why IPCC may be asserting a
time constant of some 120 years (though the effectively used one
is around 500 years). As one cannot add 0.297*infinite (for example the
remanent part for Joos IPERT), may be they only took the other terms: (0.135*507
+0.366*16.5 +0.202*3.05) / (0.135 +0.366 +0.202) = 106.8 years.
Do you think I am right - or do you know another explanation?
I am still wondering about IPCC's very high CO2 lifetime.
It may indeed have been calibrated from observed C-14 transport, for which
no Revelle factor was assumed to apply. Then Revelle=9 was taken for C-12
sequestration. It considerably reduces the uptake and thus prolongs the
eddy diffusion time needed to get into deeper ocean layers. Could this
be the reason for T being about 500 years??
With best regards,
Peter
AW: Your publications, book & carbon lifetime
Mon, 11 Jun 2001 16:42:26 +0200
From: "Volz, Dr. Hartwig" <Hartwig.Volz@rwedea.de>
To: 091335371@t-online.de CC: jahlbeck@abo.fi>
Just a remark, what I recently wrote [in German] about
this subject (14C).
I still think that the problem has to be handled as sketched
in my first note. But a further "experiment of thought" might be more illustrative:
imagine a pre-industrial situation, 280 ppm atmospheric 12CO2. When seasonal
or temperature effects are left aside, there will be no net flow to or
from the ocean. Now an experimental trick: half of the atmospheric 12CO2
is replaced by 14CO2, whereas nothing of the 12CO2 is replaced in the ocean.
Leaving secondary effects aside (isotope effects because of different physical
properties, like diffusion constants), the system is still in equilibrium,
there will be no net flow of CO2 between atmosphere and ocean. But, you
guessed it, there will be a very rapid decline of 14CO2 in the atmosphere,
with a corresponding increase in atmospheric 12CO2. The point: the system
is in *thermodynamic equilibrium* with regard to CO2. What you are measuring
is the *kinetics* of the exchange reaction. This was the point of my message
dated May 22.
Now your model and Dietze's model are based on *thermodynamic
dis-equilibrium*. The system wants to re-establish a quasi pre-industrial
situation, approximately by a first-order-reaction at a certain rate. As
I see it, the one mechanism is connected to the other in a very complex
way that I am unable to identify by a quick look.
Regards,
Hartwig Volz
Re: Your publications, book & carbon lifetime
Mon, 11 Jun 2001 11:03:00 -0400
From: harvey@cirque.geog.utoronto.ca To: p_dietze@t-online.de
(P. Dietze)
Dear Peter:
I'm glad that you've found the figure from my book useful.
I also appreciate that you found two errors in Fig. 8.6b! You are right
that the sum of the 12C and 13C curves should add up to the total C curve,
and the total carbon curve should be the same as the ocean-only curve in
Fig.8.6a. Obviously I did not check for consistency between the two figures,
as I had no reason to expect an inconsistency since they were produced
from the same output file of the model run. As it turns out, the "total
C" curve in Fig. 8.6b was placed on a secondary axis in the Excel software,
but there is no secondary axis shown in the figure (obviously there must
have been one at some time during the evolution of the figure). This caused
that curve to be in the wrong position relative to the other curves. I
seem to recall that you had trouble with my Excel files, but I'm attaching
a corrected Fig. 8.6 just in case (feel free to use the figure as you see
fit, as long as you reference the book from which it came). Otherwise,
you can imagine the "total C curve" in Fig. 8.6b to be the sum of the 12C
and 13C curves.
I haven't read the particular IPCC results that you've
been talking about, so I can't comment on the 550 year (or whatever it
was) lifetime that you mentioned. But I'll try to get around to looking
at it. As far as getting my book, go to the website: www.pearsoneduc.com/search.html
and type in the title of the book - the system will find it and give you
all the details. Then you can order it online by selecting Europe as your
geographical region.
Best regards,
Danny
Re: [Fwd: Carbon Model Calculations - discussion updated]
Mon, 11 Jun 2001 09:32:20 -0600
From: Pieter.Tans@noaa.gov To: 091335371@t-online.de
CC: roger.hanson@jgofs.uib.no, priem@dds.nl, pastott@meto.govt.uk,
...
Mr. Dietze:
After all your effort, you still have not understood one
of the basic chemical features of ocean-atmosphere CO2 exchange... But
you do have some courage, or foolhardiness, in trying to do your learning
in public. Of course the chemistry of 14C is very
nearly indentical to that of 12C. However, the 14C decrease curve
that is always shown does not portray 14CO2, but
the normalized ratio of 14CO2 to total CO2 expressed as a "del" value.
The ratio is not subject to the Revelle factor, although individual isotopomers
are. Also, think about this one: atmospheric del-14C is decreasing while
the total atmospheric 14CO2 content is increasing. Don't give up, one day
you may figure it out. This will probably be the first and last time I
am responding to your email "publications".
Pieter Tans
Comment by Peter Dietze:
The 14C del value is indeed quite proportional to the
14C excess, as total C12 changes relatively little
during some 20 or 30 years. The Revelle factor does not apply as
the
14C del value of the GEOSECS figure has been measured in the atmosphere.
Re: [Fwd: Carbon Model Calculations - discussion updated]
Mon, 11 Jun 2001 17:08:46 -0600
From: Pieter.Tans@noaa.gov To: 091335371@t-online.de
"P. Dietze" wrote:
>
>> Also, think about this one: atmospheric del-14C
is decreasing
>> while the total atmospheric 14CO2 content is
increasing
>
> Could you please explain this - that's puzzling for
me.
After the initial burst of bomb-14C partially found its
way into the oceans and terrestrial biosphere, we have now entered a situation
in which the dilution of atmospheric 14CO2 by 14C-free fossil fuel has
a significant influence on the 14C/12C ratio in the atmosphere. Fossil
fuel emissions are almost 1%/year of the total CO2 content, or a dilution
of -10 permil per year in del-14C language. This clearly is not what is
observed. The most recent data I have seen for the rate of decrease of
atmospheric del-14C is 4 permil/yr in 1993-1997. The
ave rate of total CO2 increase is 0.4 percent/yr, or 4 permil/yr. The del-14C
value is a (normalized) ratio of 14C to total C, and therefore total atmos
14C stayed constant during 1993-1997. The second derivative of atmos
del-14C is positive, or, the rate of decrease continues
to slow down. That implies that total 14C is now going up slightly,
or soon will be.
Pieter Tans
Re: [Fwd: Carbon Model Calculations - discussion updated]
Tue, 12 Jun 2001 12:40:18 -0600
From: Pieter Tans NOAA/CMDL <Pieter.Tans@noaa.gov>
To: Peter Dietze <091335371@t-online.de>
CC: roger.hanson@jgofs.uib.no, priem@dds.nl, pastott@meto.govt.uk,...
Mr. Dietze:
I wish to apologize to you for the
tone of my email response to you yesterday. That was not necessary.
I will admit to being alternately amused and exasperated by
your stubbornness in holding on to ideas that
are known to be wrong.
You have a carbon cycle model. How one deals with the
14C history is essential to an understanding of the carbon cycle. I propose
you do the following experiment. Remove as
much complexity from the model as possible by confining
the oceans to only a surface layer of a depth such that total inorganic
carbon in the oceans is the same as in the atmosphere. When your
atmosphere and ocean are in chemical and isotopic equilibrium inject
a pulse of 14C into the atmosphere by suddenly doubling the atmospheric
14C content. Watch it decay. The excess 14C will partition equally between
the atmosphere and oceanic reservoir with a time constant of about 5 years.
Then inject a pulse of CO2 into
the atmosphere, say a 20% increase. Equilibrium will be reached,
with a time constant of about 1 year, in which
the ocean's total carbon content goes up 1.8%, and
the atmosphere's 18%. The Revelle factor (well understood
chemical equilibrium thermodynamics) expresses that the ocean's acidity
increases, changing the balance between HCO3(-) and CO3(2-) ions, which
causes the oceans to resist uptake of excess CO2 proportional to what's
in the atmosphere and oceans. Isotopic ratios are
not subject to the Revelle factor because when a 14CO2 (or 13CO2) enters
the oceans a 12CO2 leaves and vice versa, not changing the pH. The pH is
only affected by the sum of all isotopomers. If the CO2 pulse you
inject is 14C-free, 14C will be coming out of the oceans until the total
atmospheric 14C is 1.073 and the oceans 0.925 of what they were originally.
(1.073/0.925 = 1.18/1.018, proportional to final total carbon reservoir
sizes). If your model does not produce these results you have a coding
error or the wrong chemical/isotopic formulation.
Pieter Tans
Re: [Fwd: Carbon Model Calculations - discussion updated]
Wed, 13 Jun 2001 12:41:48 +0200
From: "P. Dietze" <091335371@t-online.de> To: Pieter.Tans@noaa.gov
Dear Dr. Tans,
> I wish to apologize to you for the tone of my email
response
> to you yesterday. That was not necessary.
Indeed, thank you - and thanks for the well done 14C example
that you sent. Now I realize that there was a misunderstanding
between us about the Revelle factor (may be this holds for Prof. Bolin's
statements as well). I interpreted the 14C *disappearing* process
the
same way as you: after a 14 C impulse,
a fast
(thermodynamical) intermixing with the *total* C (i.e. without Revelle)
of the upper mixed layer takes place until 50:50 with the atmosphere.
Some amount of 12C will be set free into the atmosphere (should be 45%,
whereas 5% is buffered in the mixed layer, the ratio being caused by Revelle).
At
last the slower *sequestration* of both perturbations will take place responding
to the total C pressure increment - *both* being subjected to Revelle (!)
- according to some impulse response function.
You are right that a 12C impulse into the atmosphere makes
- contrary to 14C - no observable thermodynamical intermixing. As
acc. to Revelle the dynamic aux buffer capacity is only some 11%, the split
ratio will be 9:1, thus 90% are initially left in the atmosphere.
You can see this principle in my primitive basic
RC model been used for the Bern approximation by curve fitting, as well
as in my more detailed All-RC-Model, where I used a fast 33% aux buffer
which copes for light biomass and surface ground moisture as well.
Please note, that most of my considerations
have been coping with the *uptake* (sequestration) of any CO2 injection
and the *effective* e-fold time constant for sequestration. I clearly
distinguish
between buffer flux and sink flux - the CO2 which is fastly buffered
(the main buffers being the atmosphere and the upper mixed layer) is
not considered as been sequestered. The sink flux out of
these buffers (and its dynamics, represented by the time constant) is
what we are interested in because this yields our future CO2 concentration.
I am quite sure that one reason
for the dominant effective Bern time constant of about 500 years (!) is
the very high (~30%) remanent fraction, which already applies *now*
for any CO2 injection. In reality this fraction may finally be less
than 10% and may rather only apply later - same as for a reversing
of the observed strong biomass response. So for this (last) century of
fossil fuel use I think, the remanent fraction can
mostly be omitted *)
and the mean sequestration time constant for CO2 excess is indeed - as
estimated from observation - only 55 years.
Regards,
Peter Dietze
*)
Remanent fraction and Revelle increment (i.e. reduction of uptake capacity)
are counteracted by basic output from sea floor volcanoes
Re: Your publications, book & carbon lifetime
Tue, 12 Jun 2001 22:32:43 -0400
From: harvey@cirque.geog.utoronto.ca To: p_dietze@t-online.de
Dear Peter:
You are certainly right that the
IPCC reports do not explain the basics. Reading the IPCC reports
from beginning to end is not the way to learn the climate science. This
is why I wrote my book - I cover basically the same thing as IPCC WGI,
but as a textbook. It is intended to fill a niche.
You are also right that the longterm
absorption by the ocean is greater when dissolution of CaCO3 sediments
is accounted for. However, I discuss this in another section of
Chapter 8, and did point out in the text discussing
Fig. 8.6 that dissolution of CaCO3 sediments is not included. This
is because I wanted to focus on certain specific features of the ocean
response, as part of the development of the reader's thinking, and for
this reason I show only the first 200 years (when dissolution effects would
begin to be important). So maybe the 550 year lifetime
that you refer to is, as you suggest, an artefact of omitting sediment
dissolution. However, the whole concept of
a single lifetime is not very meaningful when applied to CO2, as
illustrated by this very case. It is more meaningful to talk about what
fraction of an initial impulse remains in the atmosphere after 10, 100,
200, 1000 years, as a function of the processes that are or are not included.
Regards,
Danny
Re: [Fwd: Carbon Model Calculations - discussion updated]
Wed, 13 Jun 2001 15:59:33 +0300
From: jarl.ahlbeck@abo.fi To: Pieter.Tans@noaa.gov, <091335371@t-online.de>
CC: <roger.hanson@jgofs.uib.no>, <priem@dds.nl>,
<pastott@meto.govt.uk>, ...
Dear Dr. Tans and others,
> Then inject a pulse of CO2 into the atmosphere, say
a 20% increase. Equilibrium will be
> reached, with a time constant of about 1 year, in which
the ocean's [mixed layer] total
> carbon content goes up 1.8%, and the atmosphere's 18%.
The static problem (not to be confused with my statistical
analysis of the net sink flow), water surface+atmosphere, has been solved
in my Institution (prof Westerlund) using no Revelle
factors or any other rough simplifications. Instead, we have a computerized
solution
of the numerous equilibrium equations and the charge balance involving
a numerical solution of the pH. We do not talk about pulses, we
only assume that a certain amount of carbon can be added to the total system,
and then we compute the new equilibrium, the new composition of the water
and the new atmospheric carbon dioxide concentration.
The time is involved in what we call "the
equivalent surface thickness" which is a measure of how much "backmixed"
water we have in the batch or in equilibrium with the atmosphere. Long
time=much water, short time=little water. Using 1960-2000 as a "static"
period, the model is "adapted" to reality by using known emissions and
known increase of CO2. Something about 330 m "equivalent
layer" of water is needed to balance the system for these 40 years.
When putting in a future emission scenario as IS92a and still using 330
m, the airborne fraction and the absorbed fraction remain both constant
at about 50%. Dynamics can be taken into account by assuming that
the "equivalent" layer will increase in the long run (more years
than 40) which in fact compensates for diffusional
mass transfer between flowing surface water and deep "virgin" water.
More water means greater absorbed fraction.
If the influence of the biosphere is added (not quantified
by us), the future absorbed fraction will continue
to increase. According to TAR/TS, the absorbed fraction has been
10%
greater in the 1990:s than in the 1980:s. This cannot
be explained by our static model as both periods are ten years and
hence should be connected to the same amount of equivalent ocean water
and the emissions for both periods should give about the same absorbed
fraction. So some mass transfer dynamics and biospheric influence should
be involved anyway, but this is difficult as the static model is complicated
enough. With our static program, the influence of
the temperature on the equilibrium can be calculated also (Coke
Bottle effect).
If you want more information of the ocean chemistry calculations,
please ask prof Tapio Westerlund <tapio.westerlund@abo.fi> for information.
He has
created the computer routines that are mainly used for
other purposes than ocean-atm. calculations.
Cheers, Jarl
vvv update: 29 August 2001
Your Daly arguments with IPCC scientists
Thu, 14 Jun 2001 14:13:26 -0500
From: Ross van Wassenhove <rvanwassenhove@hotmail.com>
To: <p_dietze@t-online.de>
forgive my lack of rigorous study of either the natural
science phenomena or the mathematical models by which you have so well
formulated some resistance to the "extreme" views of the effects of increasing
CO2 emissions.
i am a recent PhD in economics, with a BS in Chemistry,
and have devoted many years of research (and a dissertation that cites
your work several times) to this field of study. i have visited John's
site for over 5 years, reading and learning. someday you might even
look at my optimal control model. i hope to use some of your methods
in reformulating my model. but that is not the reason why i write
this. entschuldigen Sie, bitte.
somehow, i naively think some of the differences between
your work and that of the IPCC affiliates is the method of approach.
in short, IPCC seems to approach the problem from the "bottom up", while
you seem to see it from a "top down" model. as a result, they will
argue that you "ignore" certain natural-science phenomena, and you argue
that your model can reproduce their results without considering some of
their "details". the outcome of these situations is usually a mixture.
as earth scientists, it seems that the IPCC-affiliated
personnel want to make sure that they have started with the analysis of
natural phenomena in detail, so that they don't omit any particular factor
from their model, just in case it proves to be important as the process
proceeds. hence their study of these processes at the molecular level,
each one of which is modelled mathematically, then aggregated into a "mega-model"
(taking into account cross-effects, of course). after all their work, they
cannot simply believe that your model could represent all the observations
that has been accumulated.
meanwhile, you see the phenomena as a control process
that can (in the aggregate) be structured by applying those models which
have been shown to work in other scientific fields (e.g., electricity).
i would agree that the CO2 sequestration process is a control process,
but i believe the tie-in to "earth" phenomena has to be made for them to
accept your work. nicht wahr ? but, i agree with you that studying
their models takes away from time for your independent thought.
i think it is the "renegade" venue – John Daly's site
(indeed i have met Mr Daly while on a trip to Tasmania) – that these traditional
scientists find the most unappealing. they want your work to be "peer-reviewed"
(their peers most likely), and printed in journal form. this effort
sometimes takes years, as most of us in the publishing world realize.
i'm even impressed that they have responded to you via John's site:
it gives the your work and the site credibility.
thank you for your contributions.
Ross van Wassenhove
Associate Professor
Management Division
Lindenwood University
Your 2nd letter and modelling approach
Mon, 25 Jun 2001 13:08:05 +0200
From: "P. Dietze" <091335371@t-online.de> To: harvey@geog.utoronto.ca
Dear Danny,
thank you a lot for your 2nd letter now with part 1+2
of your submitted JGR-Oceans paper on your Climate-Carbon Cycle Model...
[shortened] Some days ago I ordered your book and I am really looking
forward because I am keen to find out the reason for the vast differences
in our projections. I suppose, it has to do with the Oeschger eddy diffusion
approach being used for most (85%) of the ocean CO2 uptake - being mostly
applied for upwelling (!?!) regions. Not only the very different diffusion
constants (ranging from 0.49 to 2.4 cm²s^-1), but the putative back-pressure
and gradient which I think is not necessary for the downwelling CO2 transport
in reality. Together with the resulting essential nonlinearity in uptake,
this may be a main reason for the much smaller future ocean uptake.
On the other hand, important factors like CO2 taken into
the oceans by precipitation (especially at cold latitudes) and the considerable
biomass response (land and marine) may not be properly represented as the
details are as difficult to be calculated as the global parameters are
difficult to be measured. And to me the 14C exchange and propagation seems
a quite shaky candidate for calibration, as you cannot easily distinguish
between mere transport and thermodynamical exchange (setting free the same
amount of 12C) and thus properly allocate the CO2 "uptake" that we are
interested in.
I think, the main difference between my work and that
of IPCC-related modellers is the method of approach. IPCC people approach
the problem trying to calculate all (known) details from the "bottom up",
while I see it from a "top down" model based on global uptake observations.
As a result, they will argue that I "ignore" many natural-science phenomena,
and I argue that my model can reproduce results without considering all
the details, but understanding the process as a control problem (which
can easily be modelled by electrical circuits).
Thanks again and my best regards,
Peter
Sarmiento & 30 yr mean CO2 lifetime
Mon, 06 Aug 2001 12:57:15 +0200
From: "P. Dietze" <091335371@t-online.de>
To: joos@climate.unibe.ch, Jan.Goudriaan@pp.dpw.wau.nl,
bconeill@brown.edu, wigley@meeker.ucar.edu, Enting <ige@dar.csiro.au>,
Pearman <gip@dar.csiro.au>, harvey@geog.utoronto.ca, ... (some 600 recipients)
Dear All who are interested in carbon modelling:
In a Special Report titled "Ocean
Carbon Cycle" by Jorge L. Sarmiento in C & EN, May 31 1993,
p.30, I found a surprising statement:
"Only about 40 to 50% of the carbon dioxide molecules
added to the atmosphere since 1800 have dissolved in the ocean. This
corresponds to a mean lifetime of carbon dioxide in the atmosphere of about
30 years [!!]. This accumulation of carbon dioxide in the atmosphere
has been verified by direct measurement".
As the e-fold lifetime T and the
mean lifetime are identical, Jorge Sarmiento even seems to consider
it to be less than my 55 years. So I do not understand the objections of
several IPCC-affiliated carbon modellers re my carbon model calculations
and discussion at http://www.john-daly.com/dietze/cmodcalc.htm and /cmodcalD.htm
Let me compare the results for the stabilization scenario
WRE550, taking 1.9 GtC/yr constant emissions till yr 2300 (see my Fig.6).
During the mean lifetime of 30 years the emission
is 57 GtC which would yield a constant 27 ppm increment - in contrast
to the Bern Model's 270 ppm increment which is ten
times more. Or, if we allow stabilization at the 550 ppm level,
and use T=30 yr, the admissible emissions should be 19
GtC/yr (instead of 1.9).
So the IPCC scientists who prepared the CO2 scenario responses
for the TAR may be in error by an order of magnitude
and urgent explanations are necessary as to why their mean CO2 lifetime
(compared with Sarmiento) is 300 years. I would like to mention that in
this context only the total atmosphere and no aux
buffer is used and the buffer fraction BF is 100%. As I use an aux
buffer of 33%, my BF is 75% and thus the 55 yr lifetime is higher - the
Bern Model's even becomes 570 yr, using BF=53%.
As T=30 years have been "verified by direct measurement",
it logically follows that the Bern (and TAR) parameters must
grossly contradict direct measurements.
Regards,
Peter Dietze
Re: Sarmiento & 30 yr mean CO2 lifetime
Mon, 6 Aug 2001 10:27:16 -0700
From: Ken Caldeira <kenc@llnl.gov> To: "Jorge L. Sarmiento"
<jls@Princeton.EDU> CC: p_dietze@t-online.de
Jorge,
I have gotten into arguments with Dietze in the past,
and it is futile to try to educate him. I believe
his ideological biases have blinded him to rational thought. He'll
take one quote out of context, and then refuse to look at how his statements
are inconsistent with the rest of your model results. If I were you, I
wouldn't waste my time trying to correct him.
Cheers, Ken
Re: Sarmiento & 30 yr mean CO2 lifetime
Fri, 10 Aug 2001 08:39:08 -0700
From: hugh.pitcher@pnl.gov To: 091335371@t-online.de
Did you ever stop to consider that there is an
obvious typo in the article and a one was omitted. [i.e. 30 instead
of 130 years]
Re: Sarmiento & 30 yr mean CO2 lifetime
Wed, 15 Aug 2001 22:29:02 -0400
From: "Jorge L. Sarmiento" <jls@Princeton.EDU>
To: "P. Dietze" <091335371@t-online.de>, joos@climate.unibe.ch,
Jan.Goudriaan@pp.dpw.wau.nl, bconeill@brown.edu, wigley@meeker.ucar.edu,
Enting <ige@dar.csiro.au>, Pearman <gip@dar.csiro.au>, harvey@geog.utoronto.ca,
...
Hello,
I expect that
most of you understand this already, but the 30 year mean life that Dietze
quotes from my article is the mean life of excess CO2 molecules with
respect to the input of carbon dioxide to the atmosphere, not with respect
to the removal of it. You get at this number by considering the
e-folding time scale of the atmospheric increase, but a simple approximation
is just to take the present excess carbon inventory in the atmosphere of
about
180 Pg C and divide it by the annual input of about 6 Pg C/yr.
The 300
year time scale discussed in the IPCC report refers to the removal rate.
The reason the removal time scale is so long is because it takes a long
time for the ocean to dissolve as much carbon dioxide as it is capable
of. As one indication of why this is so, the deep Pacific Ocean has a radiocarbon
content that is equivalent to an age of greater than 1000 years with respect
to the surface ocean. Most of the deep Pacific below 1000 m or so (and
the open oceans have a mean depth of about 4000 m) has
not been in contact with the atmosphere since centuries before the
industrial revolution even began. The same is true of most of the deep
Indian and Southern Oceans. Even the Atlantic, which is much more rapidly
mixed, has only very little anthropogenic carbon
below about 1500 m. In order for the ocean to take up as much atmospheric
carbon dioxide as it is capable of, we will have to wait many centuries
and even up to a millenium before these deep waters can come into contact
with the atmosphere and dissolve their quota.
The appropriate
numbers from my paper to compare with the IPCC report are
those given in the left hand column on page 34 of my article which
depict the fate of 100 molecules added to the air instantaneously as
a sum of exponentials with a series of decay times (Green's functions).
Only the ocean carbon sink is considered. 16
of the molecules will not be removed except on millenial time scales involving
ocean sediments and land weathering processes. 25
of the molecules are removed with an exponential time scale of 360
years, which is roughly where the 300 year time scale for removal
that the IPCC talks about comes from. 59 of the molecules
are removed on time scales of 1, 10, and 60 years, which correspond
to the ventilation of the mixed layer, upper thermocline, and deep thermocline
and intermediate waters of the ocean, respectively. These are the parts
of the ocean that have already had considerable interaction
with the atmosphere, and why about 40 to 50% of the carbon dioxide molecules
have dissolved in the ocean, and not a higher number. If one were
to stop putting CO2 molecules in the air today, it
would take of order 300 years for those in the atmosphere to drop
to the background level of about 16%, and even longer for additional sedimentary
processes to kick in that would reduce the CO2 by another 8% or so..
I hope this
helps.
Jorge Sarmiento
Jorge L. Sarmiento
AOS Program, Princeton U.
Sayre Hall, Forrestal Campus, P.O. Box CN710
Princeton, NJ 08544-0710
Tel. (609) 258-6585, Fax (609) 258-2850
e-mail: jls@princeton.edu
Mauna Loa Increase 2000 = 1.11 ppm
Thu, 16 Aug 2001 23:10:45 +0300
From: jarl.ahlbeck@abo.fi
To: Richard Courtney <rcourtne@uk.packardbell.org>,
"Mitchell, John FB" <john.f.mitchell@metoffice.com>, daly@john-daly.com,
...
Dear all,
Now it is there. BINGO! The Mauna Loa CO2 increase 2000
was 1.11 ppm (0,30% increase), see
http://cdiac.esd.ornl.gov/ftp/ndp001/maunaloa.co2
Thanks to CDIAC for providing the interesting numbers
that proof my Carbon Dioxide Thermometer approach to be correct. See
http://www.john-daly.com/co2-conc/co2therm.htm for the
old version published also in Energy & Environment Vol.11 No. 3 (2000).
I have also mailed to this list my improved calculations up to 1999
including a cross-correlogram that gives the maximum correlation for 6
months time delay for the CO2 response to temperature change. I obtained
a correlation of abt. 0.75 between MSU and CO2 increase, but only a correlation
of 0.4 for Jones-surface and CO2 increase... [shortened]
I do not think that the IPCC CO2 modellers are so found
of this result either. I do not care for media "CO2 increase
slowing down....." is not a good headline. The correct headline would be:
"More indications of high reliability for the satellite temperature record".
Cheers Jarl
Re: Mauna Loa Increase 2000 = 1.11 ppm
Fri, 17 Aug 2001 06:56:19 EDT
From: Jack1Barrett@cs.com To: jarl.ahlbeck@abo.fi, rcourtne@uk.packardbell.org,
john.f.mitchell@metoffice.com, daly@john-daly.com, ...
Dear Jarl et al.,
The recent data do fit very well with your ideas. I have
done correlations similar to yours. The correlation coefficient for the
annual CO2 increase against the 'Jones' data from 1960-2000 is 0.63, that
for the CO2 increase against satellite data is 0.7 for the years 1979-2000.
It is clear that in cool years like 2000 more CO2 dissolves in the oceans
and it does seem that the same factor is connected with the annual May-Oct
decrease in CO2 concentration (as the Southern hemisphere cools, more CO2
dissolves) as well as the greening of the Northern Hemisphere. I
still support the Peter Dietze 38 year half-life for the excess CO2 in
the atmosphere (the excess over the pre-industrial equilibrium value).
The very slow sink to the deep ocean is of importance only to the academic
calculation of when that equilibrium will be established again (after humans
become extinct)! In the meantime limestone is deposited in various parts
of the world to maintain the secular equilibrium of the upper layer of
the hydrosphere. Box 3.3 of TAR is misleading (wrong) and is a superficial
treatment of the problem. The calculation of the
fates of 100 CO2 molecules would be more interesting and realistic if all
sinks were to be considered. The competition for them by the oceans
and vegetation is critical to the understanding of their fate. If
they find their passage into the deep oceans blocked by a slow process
they will take an easier way out and assist vegetation growth.
TAR Fig 8.15 should have a plot of the GHG-alone simulation,
but it doesn't. It would be helpful to have such a plot.
Cheers, Jack
Re: Sarmiento & 30 yr mean CO2 lifetime
Tue, 21 Aug 2001 10:35:59 EDT
From: Jack1Barrett@cs.com To: 091335371@t-online.de,
jls@splash.princeton.edu
CC: joos@climate.unibe.ch, Jan.Goudriaan@pp.dpw.wau.nl,
bconeill@brown.edu,...
Dear All,
Peter is quite right. The figures for any one year are
seriously affected by the temperature of the Southern Hemisphere. A cool
year means more take-up of CO2 and a smaller time constant, but overall
Peter's half-lifetime of 38 years (and Jarl's) represents the general situation.
The figures are not to be confused with the overall residence time of CO2
which is 780 GtC (present content) divided by the total annual CO2 flux
of about 230 GtC which gives 3.4 years.
Cheers, Jack
Re: Sarmiento & 30 yr mean CO2 lifetime
Tue, 21 Aug 2001 15:27:59 +0200
From: "P. Dietze" <091335371@t-online.de> To: Jorge
Sarmiento <jls@splash.princeton.edu>
CC: joos@climate.unibe.ch, Jan.Goudriaan@pp.dpw.wau.nl,
bconeill@brown.edu, wigley@meeker.ucar.edu, Enting <ige@dar.csiro.au>,
Pearman <gip@dar.csiro.au>, harvey@geog.utoronto.ca, jochem@isi.fhg.de,
...
Dear Prof. Sarmiento,
thank you very much for your response on 15 Aug - in spite
of Ken Caldeira telling you, it is futile to try to educate me and not
to waste your time attemting to correct me. Though your article "Ocean
Carbon Cycle" [C&EN, May 31, 1993] explained your ocean model quite
well, your response was helpful for a deeper understanding. Such basic
and explaining papers are indeed so far missing among IPCC's documents.
Re the "lifetime" of CO2 - ok, if you had really meant
the
30 years to be related to the input rate excess/emission=180/6=30 yr,
so let it be. But then, please accept as well my simple calculation for
today's numbers as follows: Excess with 90 ppm: 190 GtC, total anthropogenic
emissions: 8.4 GtC, averaged airborne fraction: 38% or 3.2 GtC, sink flow:
5.2 GtC. So I get
Input
T1=190/8.4 = 22,6 yr Removal T=190/5.2 = 36.5 yr
Leaving out fast aux buffers such as surface water and
light biomass for the excess, i.e. only taking the
atmosphere and assuming that the rest of the natural carbon cycle is in
equilibrium and thus considering only anthropogenic perturbation, the observable
removal lifetime of CO2 is 36.5 years only. This time constant is
as well called adjustment time or mean lifetime
(not to be mixed up with the turnover or residence time). My figure matches
the 37.9 years obtained by Dr. Ahlbeck from regression analysis. So I do
not understand how IPCC modellers got around 300
(that you admitted), 360 or even some 500 years now been effectively applied
for the Bern model responses in the TAR - and why IPCC is misleading
people, stating that their models use a mean lifetime of about
120 years.
Be aware that the removal flux is excess/T (this is how
you can as well calculate the equilibrium emission), and so this
becomes ten times too small if T is ten times too high. I cannot
understand how IPCC-affiliated modellers did not get aware of this eyestriking
discrepancy. I am still wondering whether this has only to do with
the eddy diffusion model or it may simply have been caused by the (erroneous)
assumption that the total C Revelle factor does not
apply for radiocarbon which was used for uptake calibration.
In your C&EN paper the ocean model is well explained.
But I think, some important features have been left
out when applying that model for the global carbon cycle:
i) The biomass is more or less considered in equilibrium
and thus practically not represented, though it is considerably responding
at present.
ii) The remanent fraction (yours
is 16%, Joos' IPERT 29.7%, Goudriaan's 11% including biomass) has
been derived somehow from a saturated ocean
but applies from the beginning (!) - see your
box on p.34 or the G(t) function. It is assumed that the sedimentation
rate (including corals, shells and change of the biological pump) is and
stays very small. This may hold at present (except corals, shells and biomass
in nutrient-rich shallow water) as most of the deeper ocean water has
hardly been shifted from the 280 ppm equilibrium. But later the
sedimentation rate may increase considerably. For example we are already
observing the buildup of huge carbonate 'whitings'
in the Gulf.
iii) Your prevailing eddy downward diffusion of
CO2 (which mostly applies for warmer upwelling areas
!!??), hardly represents the bulk uptake which
rather takes place in cold downwelling areas
at high latitudes. This uptake - in parallel to the diffusion process -
is mostly proportional to the CO2 partial pressure increment and will be
more dominant as soon as the diffusion slows down. And by deep water formation
part of the abyss water has indeed been well in contact
with the atmosphere.
iv) The ocean model obviously does not cope with
inceasing CO2 removal by precipitation (especially
at cold latitudes), the CO2 uptake of polar ice
and the CO2 removal from rivers.
These points obviously cause a far too small CO2 removal
rate.
Best regards,
Peter Dietze
Re: [Fwd: Sarmiento & 30 yr mean CO2 lifetime]
Thu, 23 Aug 2001 14:53:06 -0400
From: "Steven C. Wofsy" <scw@io.harvard.edu> To: <091335371@t-online.de>
Your comments represent a fundamental
misunderstanding of the carbon cycle, one that seems to be prevalent
and, unfortunately, propagated by the IPCC. The CO2 put into the atmosphere
interacts with many parts of the earth system, including vegetation, oceans,
soils etc. These may be thought of as each taking
up and releasing carbon with their own dynamics. The result is that
it is fundamentally incorrect to assign a single
lifetime to carbon dioxide released to the atmosphere.
If you imagine a simple experiment where 1 Pg of CO2 is
released suddenly to the atmosphere, the CO2 concentration will rise by
0.5 ppm, then begin to decrease. The initial rate
of decay would fit a lifetime of 25-30 years. However, as time goes
on, the rate of dcrease slows down. At 100 years, the rate of decay would
correspond
to a lifetime exceeding 100 years. This behavior is due to rapid
equilibration of the fast-turnover reservoirs (e.g. forest litter) and
slow equilibration of the slow ones (also, the big ones, like the ocean).
Thus the increase of CO2 over time, due to chronic emissions,
is regulated by the slow turnover times, but the year-to-year variations
are regulated by the fast ones. It s completely incorrect
to assume that CO2 emissions to the atmosphere are removed with a lifetime
of 30 years, or even 55 years.
The above is not really a matter of debate, although the
actual dynamics and exchange times are certainly matters of current research.
Steven C. Wofsy
Abbott Lawrence Rotch Professor of Atmospheric and Environmental
Chemistry
Harvard University
Pierce Hall, Room 110D, 29 Oxford St., Cambridge, MA
02138
email: Steven_Wofsy@harvard.edu
Telephone: 617-495-4566 FAX: 617-495-4551
Re: [Fwd: Sarmiento & 30 yr mean CO2 lifetime]
Sun, 26 Aug 2001 12:46:05 +0200
From: "P. Dietze" <091335371@t-online.de> To: Steven
Wofsy <scw@io.harvard.edu>
Dear Prof. Wofsy,
thank you for your response and interest in the carbon
cycle topic. I read as well your "Where has all the
carbon gone?" in Science 22 June.
I think, you are essentially misunderstanding my putative
"fundamental misunderstanding of the carbon cycle". The problem is that
you seem not being familiar with dynamic system responses - as I am, who
(as electrical & control engineer) has worked intensively about this
topic in his master thesis.
You seem to assume that only a fraction
of the emitted CO2 is removed within some 30 years whereas the rest has
a tag "My lifetime is 100 to 360 years". This fraction - so the
imagination of IPCC modellers - will slowly accumulate within the atmosphere.
Thus the concentration will forever increase, showing a growing airborne
fraction (whereas it has already decreased to a mean
of 38% and even been 28% in yr 2000). The IPCC approach is completely
illogical. If we now (after 130 years since industialization) emit a CO2
impulse, you expect that the natural sinks remove
the "new" first part very fast while at the same time keeping the "old"
CO2 for centuries.
This is impossible because nature cannot discriminate
the age of the CO2 and has to treat all CO2 in the
same way. There is only one total buffer and only one (observable)
global sink flow and thus one mean (e-fold) lifetime
- no matter whether thousands of different removal processes are contributing
at different time scales. All these can be put together.
Let me give you a simple example using the mean lifetime
of humans. Assume, it is 70 years. Assume, in equilibrium, 100 million
babys are born per year. So the equilibrium population will be 7000 million.
The death (or removal) rate will be 7000 million/70=100 million per year.
According to your understanding all this cannot be stated because each
human has a different lifetime and there are many different causes for
death like accidents, diseases, civil war etc.
Re CO2 you should be aware that parallel
removal processes with different time scales can be put together as follows:
T
= 1/ (1/T1 + 1/T2 + 1/T3 + ...)
Here the smallest T process takes the lead, and sinks
with larger T have a minor removal effect. If we have a set of serial
removal processes - as assumed in the IPCC ocean layer model - we can allocate
an e-function for a mean lifetime T as follows
[typos corrected]:
G(t)
= a*exp(-t/T1) + b*exp(-t/T2) + c*exp(-t/T3)
G'(t)
= (a+b+c)*exp(-t/T) with T
= (a*T1+b*T2+c*T3)/(a+b+c)
The G'(t) function of course doesn't yield the same impulse
response as G(t), but for a long series of impulses (like our yearly emissions
over a century) the response curve for the CO2 concentration is
practically the same as with G(t). Calculations with the mean lifetime
T hold in special for all equilibrium considerations.
In the real world we have a combination
of serial (ocean eddy diffusion) and parallel (biomass, ocean deep water
formation, precipitation) removal processes. The parallel one with
the smallest T of some 37 to 55 years - this is the deep water formation
at high latitudes - takes the lead. If you would have read my "Carbon
model calculations" and followed the discussions at John Daly's
guest site http://www.john-daly.com/guests.htm, you wouldn't have made
such unqualified statements as "It is completely incorrect to assume that
CO2 emissions to the atmosphere are removed with a lifetime of 30 years,
or even 55 years" which can be falsified by simple
observation.
Regards,
Peter Dietze
Re: [Fwd: Sarmiento & 30 yr mean CO2 lifetime]
Sun, 26 Aug 2001 14:19:49 -0400
From: "Steven C. Wofsy" <scw@io.harvard.edu> To: <091335371@t-online.de>
Actually, I am quite familiar with dynamical systems.
The CO2 system acts like a coupled linear system with non-linear feedbacks
(your "serial" system). Stocks of carbon in ocean deep waters, versus
peatlands, cannot be considered one reservoir or species, like a population
of humans. The solution to this problem, ignoring feedbacks, is the one
you wrote down,
G(t) = a1*exp(-t/T1)
+ a2*exp(-t/T2) + ...
(you forgot the minus sign – all of the eigenvalues of
this problem are negative, and one may be zero (conservation of mass) or
some other small number that depends on long-term permanent removal from
the ocean-atmosphere system). Each term represents the response of one
of the eigenvectors of the system to the forcing that's imposed. The atmosphere
is not by itself an eigenfunction, so an atmospheric input excites the
others (they are not orthogonal, so this is in general the case). Thus
some fraction of the impulse decays with time constant T1, another with
T2, etc. Physically this just means that elevated CO2 in the atmosphere
partitions to many different places, e.g. peatlands, oceans,....
[comment by P. Dietze: G(t)
represents the impulse response of one serial sink (diffusive
ocean layers). For parallel sinks (e.g. peatlands, forests, downwelling
ocean) such a response with fixed partitions is impossible as each
sink is in full contact with the well mixed atmosphere. This results in
dynamic partitioning: the fastest sink takes away more and more of the
CO2 excess as time proceeds, so the slow sinks and remanent fractions become
irrelevant. Here G(t) = exp(-t/T) has to be applied with only one T
which is equal to 1/ (1/T1 + 1/T2 + 1/T3 + ...)]
The ocean, the land biosphere, and the soils all
have long response times that show up in the Ti time constants. The time
constant for the eigenvalue with the longest response (other than conservation
of mass or permanent removal to the lithosphere) is dominated by the oceans,
with a value between 150 and 600 years. The one corresponding to soils
gives 90-120 years, depending on what you think are the underlying processes.
Thus I agree with much of what you wrote, taking exception
only with the values you seem to think apply to the longer time constants,
and to the condescending remarks.
One problem in all of this is that nature does not know
that the carbon cycle is supposed to be like these linear models, no matter
how realistic we try to make them. If we look at the the details of the
ice core record, and the more indirect records from marine sediments, we
see that concentrations of CO2 have on occasion risen rapidly, but decreases
are generally quite slow. This tells us something, don't you think?
Steven C. Wofsy
Re: [Fwd: Sarmiento & 30 yr mean CO2 lifetime]
Mon, 27 Aug 2001 09:34:12 +0200
From: "P. Dietze" <091335371@t-online.de> To: "Steven
C. Wofsy" <scw@io.harvard.edu>
Dear Prof. Wofsy,
thanks for your fast and mostly positive response on Sunday.
I am sorry, because I was in a hurry to go out, I made a few typing errors
in G(t) and G'(t). Of course, all exponentials must be as exp(-t/Ti). The
resulting mean lifetime for serial sinks is
T = (a*T1+b*T2+c*T3)/(a+b+c).
Re the partly very large lifetimes of IPCC's serial sink
fractions, please be aware that we have to cope with
other (faster) parallel removal processes. If I consider a bucket
of water with two holes, a very small one and a big one, it
is not the small hole that keeps the water in the bucket for long, but
it is the big hole that removes it fast.
I think, after we are now emitting vast amounts of CO2
for over a century, we should be able to clearly observe
the characteristics of the IPCC eddy diffusion model - decreasing uptake
and increasing airborne fraction. But the opposite occurs - and
IPCC is not willing to admit that and correct their models, for political
reasons.
Regards,
Peter Dietze
CO2 regression analysis
Mon, 27 Aug 2001 12:42:16 +0300
From: <jarl.ahlbeck@abo.fi> To: Peter Dietze <091335371-0001@t-online.de>
Hello Peter,
found good deforestation data now, Houghton 1999 in Tellus
51B:298-313. My former emissions were only from fossil+cement as I did
not know the deforestation rate. Moreover, as you suggested, I have now
coped with your 33% fast buffer, added to the storage capacity of the atmosphere.
After I had redone my Fortran program to solve the compiler problems and
removed some errors, I could finally run some successful tests and the
regression analysis that you wanted. I use a non-linear Fortran routine
made by myself, SIMPLEX-search equations originally presented by David
M. Himmelblau in "Process analysis by Statistical Methods", Wiley &
Sons 1972. I used my - the best available - emission data from 1970 to
2000. I have not invented any single data number by myself. All data are
from the literature + standard regression routines. Here is the equation
on which the nonlinear regression analysis (least square search) for your
excess CO2 e-fold lifetime T is based:
Sink
= (1-1.33*Af)*Em =1.33*2.123*(C-C0)*(1/T)
with Af: airborne fraction, Em: total emission including
land use, C0: preindustrial 280
ppm, C: observed smoothed concentration.
Regression analysis by the computer gives T=
55.020 years
Cheers, Jarl

This paper: http://www.john-daly.com/dietze/cmodcalD.htm
Return to Climate
Guests Papers Contents Page
Return to "Still
Waiting For Greenhouse" Main Page





