|
REGIONAL TEMPERATURE CHANGE by Vincent R. Gray (updated 2nd April 2003) Climate Consultant Email: vinmary.gray@paradise.net.nz
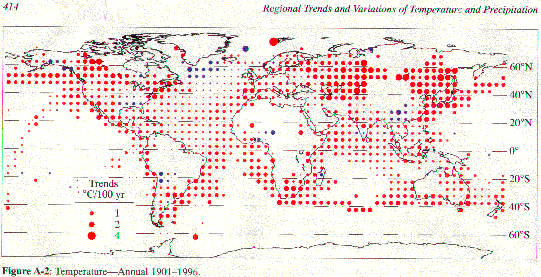
ABSTRACT Data compiled by Karl (1998) of the temperature changes between 1901 and 1996 for 5°x5° grids on the earth’s surface, have been divided into smaller regions than those used by him, and the mean temperature change for each region calculated. It is found that the data show large differences in the temperature change between 1901 and 1996 for different geographical and political regions. The extreme ranges (6.17°C between individual 5°x5° boxes, and 1.96°C between regions) are large enough to cast doubt on measurements, such as those from ice cores and tree rings, taken in only a few places, and also on values for mean temperature change from the data considered here, which omit several important regions. A feature of the results is the large temperature increase in the former Imperial Russia/ Soviet Union (+1.23°C), more than double the change in Western Europe (+0.5°C) or the USA (+0.41°C). This large temperature rise in Russia/Siberia by so many stations that were regarded by Peterson et al (1999) as predominantly “rural”, casts doubt on their assumption that the effects of local heating in rural stations are negligible. Removal of the Russia/Siberia set from their analysis would surely show a significant urbanisation effect from cities in the rest of the world. This widespread local heating around surface measurement stations would explain the differences between the surface temperature record and temperature measurements in the lower troposphere by satellites., and so the major human influence on the climate There is a large positive temperature change gradient of about 0.9°C from the North to the South Atlantic and several small regions show a temperature fall. Karl’s (1998) data suffer from many limitations.. There are only a few continuous records, with notable gaps during the two world wars, and several apparently anomalous results which may indicate inadequacies of measurement. These limitations would appear to derive from the accepted surface measurement datasets of Jones (1994) and Folland and Parker (1995) INTRODUCTION According to the IPCC (Intergovernmental Panel on Climate Change), (Houghton et al 1996), the mean surface temperature of the earth’s surface has increased by about 0.3 to 0.6°C since the late 19th century, and by about 0.2 to 0.3°C over the last 40 years, although, recently, Jones (1998) speaks of “the 0.6°C global warming during this century”. Regional variation of this temperature rise has, however, not been entirely clear, despite studies, some of which contained coloured maps, of Hansen and Lebedeff (1987), Jones and Briffa (1992) Parker et al. (1994). Houghton et al (1996), and Jones et al. (1997). Karl (1998) in Annexe A, of the IPCC report Regional Trends and Variations of Temperature and Precipitation (Figure A-2 in that report) showed the temperature change between 1901 and 1996 on a Mercator map of the world by means of coloured dots for each of the geographical grids of 5° x 5° for which acceptable measurements are available. The size of the dot inside each grid indicated the size of the measured temperature change. There were red dots for a temperature rise and black dots for a temperature fall.
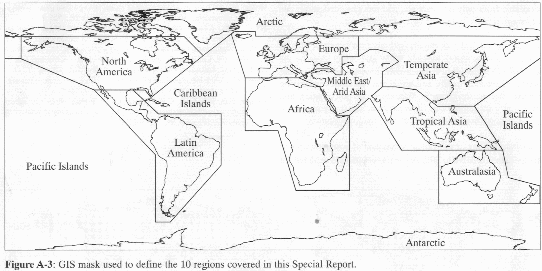
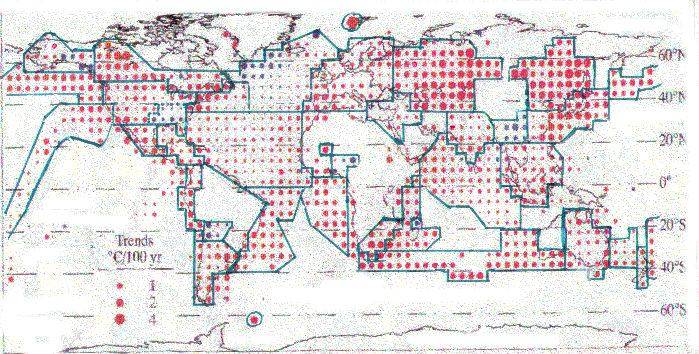
The dataset, which consisted of mean annual temperature anomalies from 1901 to 1996, with regard to the 1961-1990 average, for 5°x5 grids on the earth’s surface, was then used to provide individual mean annual temperature anomaly figures for each of 12 regions to give a plot of its temperature history from 1901 to 1996. . The regions chosen by Karl were rather large, and usually spanned over several geographic and political boundaries. Also, they did not include some oceans. This paper divides the same data into smaller regions, based on better defined geographic and political boundaries, and calculates the mean temperature change for each region in the same manner as that carried out by Karl (1998), in an attempt to throw more light on the details of regional temperature change.
REGIONAL TEMPERATURE TRENDS 1901-1996
Table 2. Regional Temperature Change 1901-1996 (Data from Karl (1998))
Totals 827 40.33 (Note: South-East USA is a subset of Continental United States) Perhaps the most interesting results from the above subdivision of Karl’s temperature data are the temperature change figures for the former Russian Empire/Soviet Union. West Siberia/Russia showed a mean temperature rise, 1991 to 1996 of +1.19°C for 59 grids, representing 2.17% of the earth’s surface, and East Siberia showed a mean temperature rise of 1.30°C for 39 grids, 1.50% of the earth’s surface. The combined figure for Russia/Siberia is a rise of 1.23°C for 3.67% of the earth’s surface. This compares with a rise of only 0.51°C for Western Europe (50 grids, 1.84% area) and 0.41°C for the Continental United States (36 grids, 1.67% area). These Russia/Soviet results distort conclusions about global temperature change. For example, Peterson et al (1999) found that global rural temperature trends did not differ significantly from overall global temperature trends. They concluded that this meant that both sets were free from local heating, whereas it actually means that both sets are equally affected by local heating. Most of the Russia/Soviet data would have been classified as “rural”, and their high figures would have counterbalanced a probable lower temperature trend of rural sites as compared with urban sites in other parts of the globe. Omission of the Russia/Soviet data from the rural sites studied by Peterson et al 1998 would surely show that elsewhere in the world there was a significant “urbanisation” effect in urban sites. The evident local heating around measurement sites, particularly in cities and in cold rural sites, would explain the differences between the surface temperature record and that of the lower troposphere, as determined by satellites and thus account for the human influence on surface temperatures The high Russia/Soviet figures indicate a common trend of large temperature rises in remote rural sites in severe climates. Other examples are Canada minus W Yukon (+0.96°C), North Pacific (+0.90°C) Spitzbergen (+4.06°C) and South Georgia (+1.91°C). The main reason would surely be the pressure to improve living conditions in these remote sites, involving better heating in the buildings, provision of roads, and the tendency for vegetation around the sites to be encouraged. The narrowing of the diurnal temperature range for many of these sites (Easterling et al. 1997) is further evidence for this tendency. An additional possibility for the Russia/Soviet sites is that as many are at, or close to prison camps rations and food in the 1920s might have depended on claims of low temperatures.
DISCUSSION The data consist of those series for which there are at least 72 observations out of a possible 96. The temperature change from 1901 to 1996 was calculated by Karl (1998) by subtracting the average of the first five figures from the average of the last five figures. Of the 938 records, only 297 are complete, and only 619 begin in the year 1901. Two of them do not start until the year 1925. The figures do not therefore strictly represent the temperature change over the whole period 1901 to 1996. Of the up to 24 missing annual readings in each record, most are in the 1914-1918 and 1940-1945 years. 81 records have missing readings for the whole period of 1914-1918 and 40 records have missing readings for 1940-1945. 412 (44%) readings are missing for 1918 and 236 (25%) in 1945. Examination of the data shows that almost all of the 1901-1996 temperature rise for Russia/Soviet Union took place in one year, 1987 to 1988. Table 3 gives the details. The average rise for the whole of the region was 1.21°C which contributes 0.16°C to the Northern Hemisphere for that year, and 0.10°C to the Global temperature increase. Since the recorded temperature increase for the Globe is 0.02°C, this means that without the Russian figure, there would have been a fall of 0.08°C. TABLE 3 Change in Annual Mean Temperature, °C, between 1987 and 1988 for West Siberia/Russia, for 5°x5° grids, according to Karl (1998)
Karl’s data show that there are large differences in the temperature change from 1901 and 1996 between different regions on the earth’s surface. Individual 5°x5° grids .ranged between -2.12°C in the Greenland Sea and +.4.06°C for Spitzbergen (only 1500 km away) Larger regions ranged from -0.46°C for Bolivia to +1.30°C for East Siberia.. One has to question whether studies based on only a few regions, for example those from ice cores or tree rings, can give an adequate estimate of global temperature change. There is only a slight difference between the Northern and the Southern Hemisphere, but is this apparent agreement real? Only 31.4% of the Southern Hemisphere had acceptable measurements. The most comprehensive series of measurements were those made in the Atlantic Ocean. Here there was a marked positive temperature change gradient between the north and the south; from -0.11°C for the North Atlantic, to 0.64°C for the north east Atlantic, to 0.44°C for the Middle Atlantic, 0.75°C for the South East Atlantic and 0.84°C for the South East Atlantic. There is a similar positive gradient between the Arabian Sea/ Bay of Bengal (0.53°C) and the sea route Capetown to Australia (0.91°C) If the results from these oceans are combined with comparisons between land measurements in Western Europe (0.50°C) and the USA (0.40°C), in the Northern Hemisphere, and with South Africa (0.76°C), Eastern Australia (0.64°C) and Chile/Argentina (0.67°C) in the Southern Hemisphere, a case can be made for a greater temperature increase in the Southern Hemisphere than in the Northern Hemisphere. This change is, however, counteracted by the very large positive temperature change in the former Imperial Russia/ Soviet Union. Russia/Western Siberia was 1.19°C and Eastern Siberia 1.30°C.. The conclusions from the overall figures that there was little or no difference between the temperature changes of the Northern and Southern Hemispheres between 1901 and 1996, and that the mean temperature change in the Northern Hemisphere over that period was 0.58°C, are heavily dependent on the Russian results. It is unfortunate that measurements in the Pacific Ocean are so sparse. The mean temperature change in the North Pacific was high, at +0.90°C . The sea route from North America to Auckland had a mean temperature change figure of + 0.65°C, and there was a marked fall in the temperature change from North to South. Several of the sparse measurements near the centre of the ocean were negative. It looks as if there may have been a fall in temperature change from north to south , but with so much of the area not measured, this conclusion must be tentative. Falls in temperature were recorded in the North Atlantic (-0.11°C), Alaska/Yukon (-0.12°C), South Greenland (-0.44°C), SW China/ Tibet (-0.44°C), SW United States (-0.37°C), Bolivia (-0.46), Nigeria (-0.43°C) and in Madagascar (Tananarive) (-0.61°C). The last two need to be questioned. The five low points in Nigeria are next to a neighbouring point of +1.46°C in Timbuktu. Madagascar is surrounded by sea with a temperature rise of +0.64°C. Also, there were no records for Tananarive between 1916 and 1931. The most extreme example in Karl’s dataset is the stated mean annual temperature anomaly for 77.5N. 12.5E (Spitzbergen) for the year 1917 of -7.63°C, when only 1500 km away in the Greenland Sea, the value was -0.03°C.
The data do not cover major regions of the globe. These include almost all of the Pacific Ocean, the Southern Ocean, the South Indian Ocean and South China Sea, most of Africa, Brazil, Central Siberia, the Arctic and Western Australia. The results for the Southern Hemisphere are particularly sparse. If it turned out that there was some doubt over the Russian/Soviet figures, then a positive temperature trend between the Northern and Southern Hemisphere, as shown by the Atlantic Ocean, could exist, as predicted by the cooling effects of sulphate aerosols, which should be greater in the Northern Hemisphere. The fact that many of the data are missing from the 1914-1918 and 1939-1945 periods, raises doubts about the continuity of data in many 5°x5° grids, where measurement sites would probably have changed personnel, location and instrumentation over the period. The limitations of Karl’s dataset would appear to apply also to the widely accepted surface temperature record from which it was derived (i.e. Jones 1994, Parker and Folland 1995)
CONCLUSIONS More detailed subdivision of Karl’s (1998) data into smaller regions indicates that there is much greater regional variability in temperature change than has been previously recognised. This casts doubt on the representativeness of surface temperature measurements made in, or derived from only one or a few places. Karl’s (1998) data suffer from a number of limitations which affect these conclusions, as well as those of his own study. Since these limitations must also be associated with the basic data used to establish the surface temperature record, established by Jones (1994) and Folland and Parker (1995), then that record has to be questioned also. The evident local heating in rural sites in cold regions shows that assumptions about the absence of “urbanisation” are incorrect. Local heating effects undoubtedly occur in both urban and rural sites, and they go far to explain the discrepancies between the surface temperature record and that of the lower troposphere, as measured by satellites. This represents a major part of the supposed “ human” influence on the climate. REFERENCES Easterling, D.R., T.C. Peterson, T.R. Karl. D.E. Parker, M.J. Salinger, V. Razuvayev, N. Plummer, P. Jamason, and C.K. Folland, Maximum and minimum temperature trends for the globe. Science 277 365-367, 1997 Folland, C.K and D.E. Parker, Correction of instrumental biases in the historical sea-surface temperature data. Quarterly Journal of the Royal Meteorological Society, 121, 319-367, 1995. Hansen, J. and S. Lebedeff, “Global Trends of Measured Surface Air Temperature. J. Geophysical Research, 92, D11; 13,345-13,372, 1987 Houghton, J.T., L.G. Meira Filho, B.A. Callander, N. Harris, A Kattenberg, and K. Maskell, Eds.. Climate Change 1995: The Science of Climate Change Cambridge University Press, for the Intergovernmental Panel on Climate Change. 1996 Jones, P.D., 1994, Hemispheric surface air temperature variations: a reanalysis and an update to 1993. Journal of. Climate 3, 1794-1802. Jones, P.D. 1998 “It was the best of times, it was the worst of times” Science 280 544-545. Jones. P.D. and K.R. Briffa, K.R., Global surface air temperature variations during the twentieth century: Part 1.” The Holocene 2,2 165-179, 1992 Jones. P.D., T.J. Osborn, T.M.L. Wigley, P.M.Kelly and B.D. Santer, Comparisons between the microwave sounding unit temperature record and the surface temperature record from 1979 to 1996: Real differences or potential discontinuities. J Geophysical Research,102, D25, 30,135-30,145., 1997 Karl, T.R., Annexe A ; Regional Trends and Variations of Temperature and Precipitation, in The Regional Impacts of Climate Change ( R.T. Watson, M.C. Zinyowera, and R.H. Moss, Eds.) , Cambridge University Press, 1998 Parker, D.E., P.D. Jones, C.K. Folland and A Bevan, Interdecadal changes of surface temperature since the late 19th century. Journal of Geophysical Research 99, 14373-14399, 1994. Peterson, T.C., K.P. Gallo, J. Lawrimore, T.W. Owen, A. Huang, and D. McKittrick . Global rural temperature trends. Geophys. Res.Letters 26, (3) 329-332., 1999 Submitted (as amended) to Geophysical Research Letters, December 7th 1999 |